Question Number 175004 by saboorhalimi last updated on 15/Aug/22
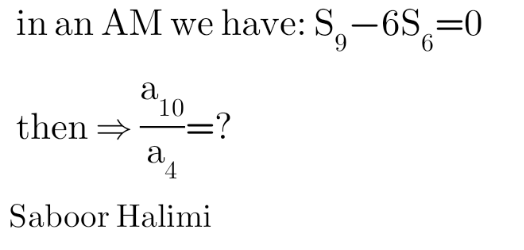
Commented by kaivan.ahmadi last updated on 15/Aug/22
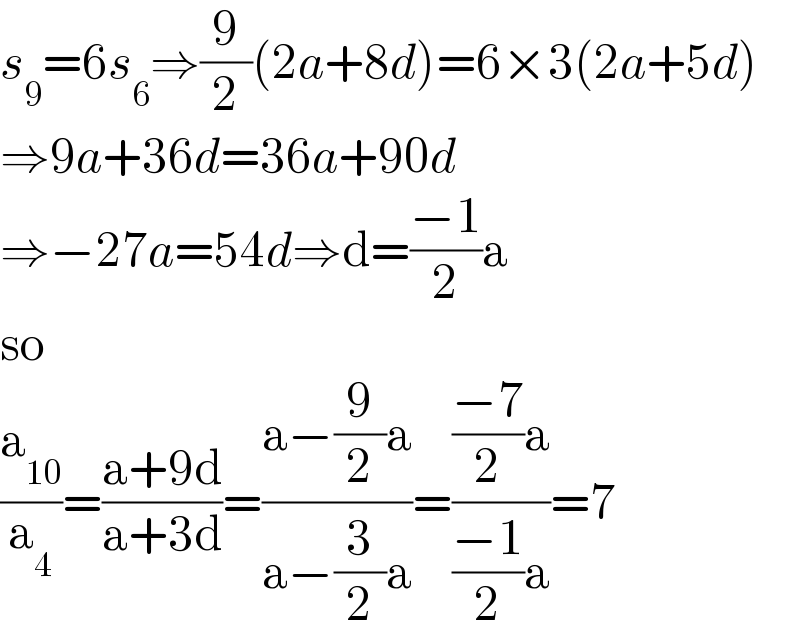
$${s}_{\mathrm{9}} =\mathrm{6}{s}_{\mathrm{6}} \Rightarrow\frac{\mathrm{9}}{\mathrm{2}}\left(\mathrm{2}{a}+\mathrm{8}{d}\right)=\mathrm{6}×\mathrm{3}\left(\mathrm{2}{a}+\mathrm{5}{d}\right) \\ $$$$\Rightarrow\mathrm{9}{a}+\mathrm{36}{d}=\mathrm{36}{a}+\mathrm{90}{d} \\ $$$$\Rightarrow−\mathrm{27}{a}=\mathrm{54}{d}\Rightarrow\mathrm{d}=\frac{−\mathrm{1}}{\mathrm{2}}\mathrm{a} \\ $$$$\mathrm{so} \\ $$$$\frac{\mathrm{a}_{\mathrm{10}} }{\mathrm{a}_{\mathrm{4}} }=\frac{\mathrm{a}+\mathrm{9d}}{\mathrm{a}+\mathrm{3d}}=\frac{\mathrm{a}−\frac{\mathrm{9}}{\mathrm{2}}\mathrm{a}}{\mathrm{a}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{a}}=\frac{\frac{−\mathrm{7}}{\mathrm{2}}\mathrm{a}}{\frac{−\mathrm{1}}{\mathrm{2}}\mathrm{a}}=\mathrm{7} \\ $$
