Question Number 4387 by Rasheed Soomro last updated on 17/Jan/16
Commented by Rasheed Soomro last updated on 17/Jan/16

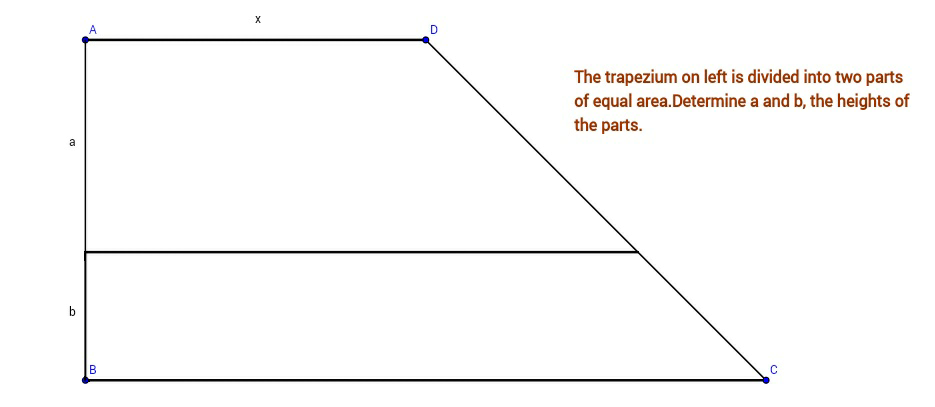
$$\mathrm{In}\:\mathrm{the}\:\mathrm{trapezium}\:\mathrm{m}\angle\mathrm{A}=\mathrm{m}\angle\mathrm{B}=\frac{\pi}{\mathrm{2}}\:\mathrm{rad}. \\ $$$$\mathrm{m}\overline {\mathrm{AB}}=\mathrm{m}\overline {\mathrm{AD}}=\mathrm{x}\:\mathrm{units}\:\mathrm{and}\:\mathrm{m}\overline {\mathrm{BC}}=\mathrm{2x}\:\mathrm{units}. \\ $$$$\mathrm{The}\:\mathrm{trapezium}\:\mathrm{has}\:\mathrm{been}\:\mathrm{divided}\:\mathrm{into}\:\mathrm{two} \\ $$$$\mathrm{sub}-\mathrm{trapeziums}\:\mathrm{of}\:\mathrm{equal}\:\mathrm{area}. \\ $$$$\mathrm{Determine}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b},\mathrm{the}\:\mathrm{heights}\:\mathrm{of}\:\mathrm{sub}- \\ $$$$\mathrm{trapeziums}. \\ $$
Commented by Yozzii last updated on 22/Jan/16
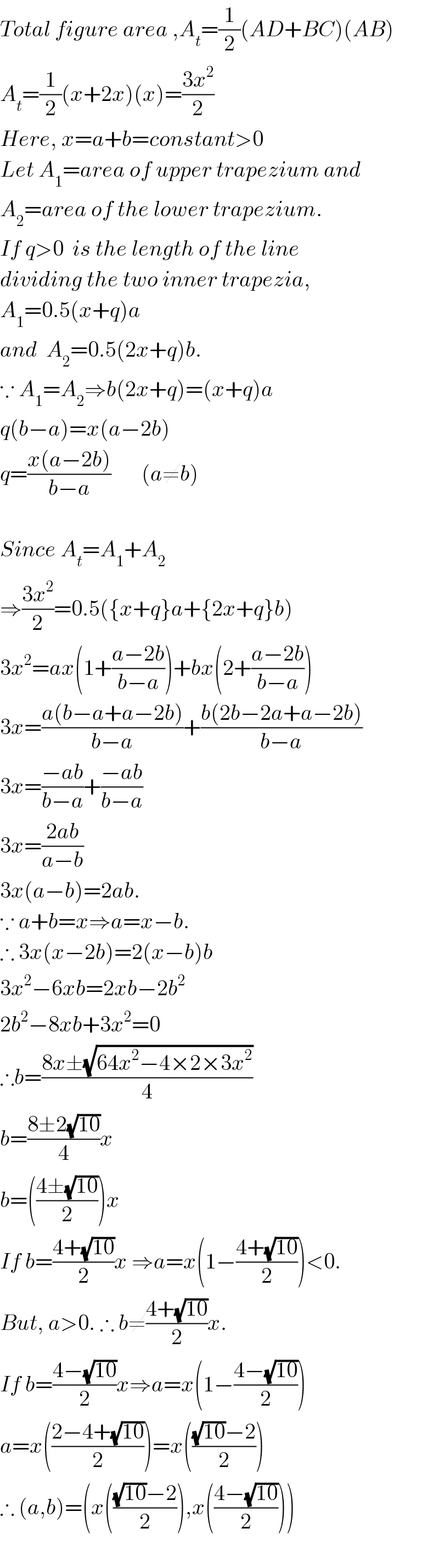
$${Total}\:{figure}\:{area}\:,{A}_{{t}} =\frac{\mathrm{1}}{\mathrm{2}}\left({AD}+{BC}\right)\left({AB}\right) \\ $$$${A}_{{t}} =\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\mathrm{2}{x}\right)\left({x}\right)=\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${Here},\:{x}={a}+{b}={constant}>\mathrm{0} \\ $$$${Let}\:{A}_{\mathrm{1}} ={area}\:{of}\:{upper}\:{trapezium}\:{and} \\ $$$${A}_{\mathrm{2}} ={area}\:{of}\:{the}\:{lower}\:{trapezium}. \\ $$$${If}\:{q}>\mathrm{0}\:\:{is}\:{the}\:{length}\:{of}\:{the}\:{line} \\ $$$${dividing}\:{the}\:{two}\:{inner}\:{trapezia}, \\ $$$${A}_{\mathrm{1}} =\mathrm{0}.\mathrm{5}\left({x}+{q}\right){a}\: \\ $$$${and}\:\:{A}_{\mathrm{2}} =\mathrm{0}.\mathrm{5}\left(\mathrm{2}{x}+{q}\right){b}. \\ $$$$\because\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} \Rightarrow{b}\left(\mathrm{2}{x}+{q}\right)=\left({x}+{q}\right){a} \\ $$$${q}\left({b}−{a}\right)={x}\left({a}−\mathrm{2}{b}\right) \\ $$$${q}=\frac{{x}\left({a}−\mathrm{2}{b}\right)}{{b}−{a}}\:\:\:\:\:\:\:\left({a}\neq{b}\right) \\ $$$$ \\ $$$${Since}\:{A}_{{t}} ={A}_{\mathrm{1}} +{A}_{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0}.\mathrm{5}\left(\left\{{x}+{q}\right\}{a}+\left\{\mathrm{2}{x}+{q}\right\}{b}\right) \\ $$$$\mathrm{3}{x}^{\mathrm{2}} ={ax}\left(\mathrm{1}+\frac{{a}−\mathrm{2}{b}}{{b}−{a}}\right)+{bx}\left(\mathrm{2}+\frac{{a}−\mathrm{2}{b}}{{b}−{a}}\right) \\ $$$$\mathrm{3}{x}=\frac{{a}\left({b}−{a}+{a}−\mathrm{2}{b}\right)}{{b}−{a}}+\frac{{b}\left(\mathrm{2}{b}−\mathrm{2}{a}+{a}−\mathrm{2}{b}\right)}{{b}−{a}} \\ $$$$\mathrm{3}{x}=\frac{−{ab}}{{b}−{a}}+\frac{−{ab}}{{b}−{a}} \\ $$$$\mathrm{3}{x}=\frac{\mathrm{2}{ab}}{{a}−{b}} \\ $$$$\mathrm{3}{x}\left({a}−{b}\right)=\mathrm{2}{ab}. \\ $$$$\because\:{a}+{b}={x}\Rightarrow{a}={x}−{b}. \\ $$$$\therefore\:\mathrm{3}{x}\left({x}−\mathrm{2}{b}\right)=\mathrm{2}\left({x}−{b}\right){b} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{xb}=\mathrm{2}{xb}−\mathrm{2}{b}^{\mathrm{2}} \\ $$$$\mathrm{2}{b}^{\mathrm{2}} −\mathrm{8}{xb}+\mathrm{3}{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\therefore{b}=\frac{\mathrm{8}{x}\pm\sqrt{\mathrm{64}{x}^{\mathrm{2}} −\mathrm{4}×\mathrm{2}×\mathrm{3}{x}^{\mathrm{2}} }}{\mathrm{4}} \\ $$$${b}=\frac{\mathrm{8}\pm\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{4}}{x} \\ $$$${b}=\left(\frac{\mathrm{4}\pm\sqrt{\mathrm{10}}}{\mathrm{2}}\right){x} \\ $$$${If}\:{b}=\frac{\mathrm{4}+\sqrt{\mathrm{10}}}{\mathrm{2}}{x}\:\Rightarrow{a}={x}\left(\mathrm{1}−\frac{\mathrm{4}+\sqrt{\mathrm{10}}}{\mathrm{2}}\right)<\mathrm{0}. \\ $$$${But},\:{a}>\mathrm{0}.\:\therefore\:{b}\neq\frac{\mathrm{4}+\sqrt{\mathrm{10}}}{\mathrm{2}}{x}. \\ $$$${If}\:{b}=\frac{\mathrm{4}−\sqrt{\mathrm{10}}}{\mathrm{2}}{x}\Rightarrow{a}={x}\left(\mathrm{1}−\frac{\mathrm{4}−\sqrt{\mathrm{10}}}{\mathrm{2}}\right) \\ $$$${a}={x}\left(\frac{\mathrm{2}−\mathrm{4}+\sqrt{\mathrm{10}}}{\mathrm{2}}\right)={x}\left(\frac{\sqrt{\mathrm{10}}−\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\therefore\:\left({a},{b}\right)=\left({x}\left(\frac{\sqrt{\mathrm{10}}−\mathrm{2}}{\mathrm{2}}\right),{x}\left(\frac{\mathrm{4}−\sqrt{\mathrm{10}}}{\mathrm{2}}\right)\right)\: \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 22/Jan/16

$$\mathcal{TH}\alpha{n}\Bbbk^{\mathcal{S}} ! \\ $$
