Question Number 175061 by daus last updated on 17/Aug/22

Commented by Rasheed.Sindhi last updated on 17/Aug/22

$$\left(\mathrm{a}\right)\:\:\mathrm{150} \\ $$
Answered by cortano1 last updated on 18/Aug/22
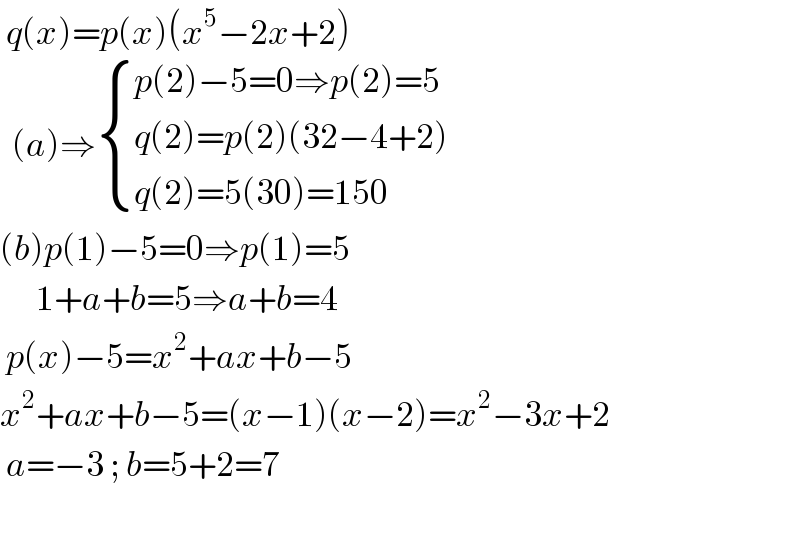
$$\:{q}\left({x}\right)={p}\left({x}\right)\left({x}^{\mathrm{5}} −\mathrm{2}{x}+\mathrm{2}\right) \\ $$$$\:\:\left({a}\right)\Rightarrow\begin{cases}{{p}\left(\mathrm{2}\right)−\mathrm{5}=\mathrm{0}\Rightarrow{p}\left(\mathrm{2}\right)=\mathrm{5}}\\{{q}\left(\mathrm{2}\right)={p}\left(\mathrm{2}\right)\left(\mathrm{32}−\mathrm{4}+\mathrm{2}\right)}\\{{q}\left(\mathrm{2}\right)=\mathrm{5}\left(\mathrm{30}\right)=\mathrm{150}}\end{cases} \\ $$$$\left({b}\right){p}\left(\mathrm{1}\right)−\mathrm{5}=\mathrm{0}\Rightarrow{p}\left(\mathrm{1}\right)=\mathrm{5} \\ $$$$\:\:\:\:\:\:\mathrm{1}+{a}+{b}=\mathrm{5}\Rightarrow{a}+{b}=\mathrm{4} \\ $$$$\:{p}\left({x}\right)−\mathrm{5}={x}^{\mathrm{2}} +{ax}+{b}−\mathrm{5} \\ $$$${x}^{\mathrm{2}} +{ax}+{b}−\mathrm{5}=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)={x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2} \\ $$$$\:{a}=−\mathrm{3}\:;\:{b}=\mathrm{5}+\mathrm{2}=\mathrm{7} \\ $$$$ \\ $$
