Menu Close

Show-that-cos-2-x-1-2-1-cos2x-

Tinku Tara 0 Comments
Pin




Question Number 44028 by pieroo last updated on 20/Sep/18
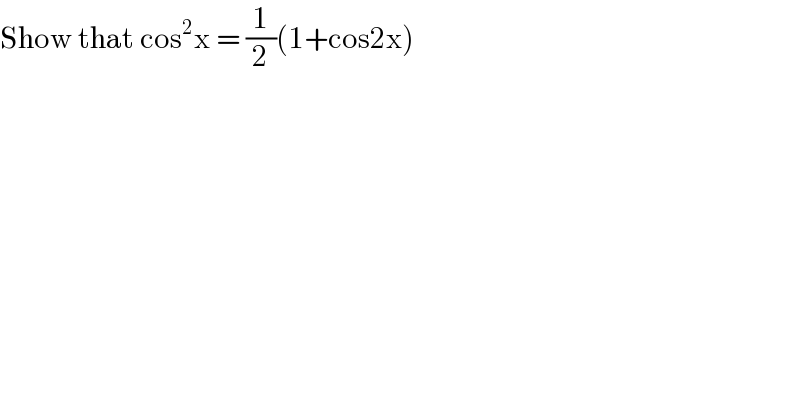
Show that cos^2 x = (1/2)(1+cos2x)
$$\mathrm{Show}\:\mathrm{that}\:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos2x}\right) \\ $$
Commented by maxmathsup by imad last updated on 20/Sep/18
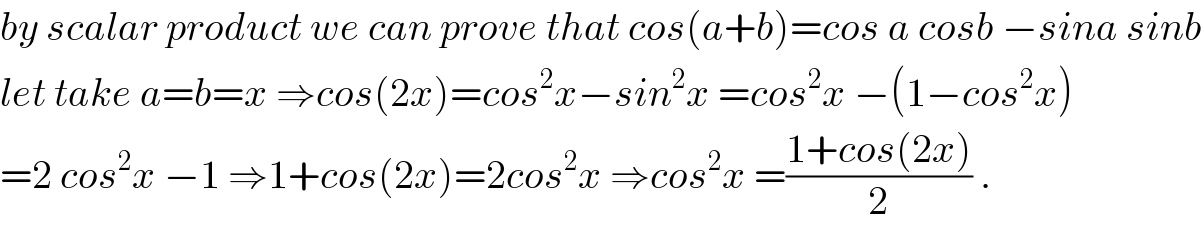
by scalar product we can prove that cos(a+b)=cos a cosb −sina sinb let take a=b=x ⇒cos(2x)=cos^2 x−sin^2 x =cos^2 x −(1−cos^2 x) =2 cos^2 x −1 ⇒1+cos(2x)=2cos^2 x ⇒cos^2 x =((1+cos(2x))/2) .
$${by}\:{scalar}\:{product}\:{we}\:{can}\:{prove}\:{that}\:{cos}\left({a}+{b}\right)={cos}\:{a}\:{cosb}\:−{sina}\:{sinb} \\ $$$${let}\:{take}\:{a}={b}={x}\:\Rightarrow{cos}\left(\mathrm{2}{x}\right)={cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\:={cos}^{\mathrm{2}} {x}\:−\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)\: \\ $$$$=\mathrm{2}\:{cos}^{\mathrm{2}} {x}\:−\mathrm{1}\:\Rightarrow\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)=\mathrm{2}{cos}^{\mathrm{2}} {x}\:\Rightarrow{cos}^{\mathrm{2}} {x}\:=\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:. \\ $$
Answered by MJS last updated on 20/Sep/18
f(x)=cos^2 x f(0)=1 f(45°)=(1/2) f(90°)=0 f(135°)=(1/2) f(180°)=1 f(225°)=(1/2) f(270°)=0 f(315°)=(1/2) so we have a periodic function period=180° or π minima=0; maxima=1 looks like a cosinus twice as fast and half as wide, shifted up so the min&max are 0&1 instead of ±(1/2) twice as fast =cos 2x half as wide=(1/2)cos 2x shifted up=(1/2)+(1/2)cos 2x =(1/2)(1+cos 2x)
$${f}\left({x}\right)=\mathrm{cos}^{\mathrm{2}} \:{x} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{45}°\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left(\mathrm{90}°\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{135}°\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left(\mathrm{180}°\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{225}°\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left(\mathrm{270}°\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{315}°\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}\:\mathrm{periodic}\:\mathrm{function} \\ $$$$\mathrm{period}=\mathrm{180}°\:\mathrm{or}\:\pi \\ $$$$\mathrm{minima}=\mathrm{0};\:\mathrm{maxima}=\mathrm{1} \\ $$$$\mathrm{looks}\:\mathrm{like}\:\mathrm{a}\:\mathrm{cosinus}\:\mathrm{twice}\:\mathrm{as}\:\mathrm{fast}\:\mathrm{and}\:\mathrm{half}\:\mathrm{as} \\ $$$$\mathrm{wide},\:\mathrm{shifted}\:\mathrm{up}\:\mathrm{so}\:\mathrm{the}\:\mathrm{min\&max}\:\mathrm{are}\:\mathrm{0\&1} \\ $$$$\mathrm{instead}\:\mathrm{of}\:\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{twice}\:\mathrm{as}\:\mathrm{fast}\:=\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\mathrm{half}\:\mathrm{as}\:\mathrm{wide}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\mathrm{shifted}\:\mathrm{up}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$
Commented by MJS last updated on 20/Sep/18
I thought it might be of interest to show it without using any formula, because the given equation is considered to be a formula itself...
$$\mathrm{I}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{might}\:\mathrm{be}\:\mathrm{of}\:\mathrm{interest}\:\mathrm{to}\:\mathrm{show}\:\mathrm{it} \\ $$$$\mathrm{without}\:\mathrm{using}\:\mathrm{any}\:\mathrm{formula},\:\mathrm{because}\:\mathrm{the} \\ $$$$\mathrm{given}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{considered}\:\mathrm{to}\:\mathrm{be}\:\mathrm{a}\:\mathrm{formula} \\ $$$$\mathrm{itself}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Sep/18
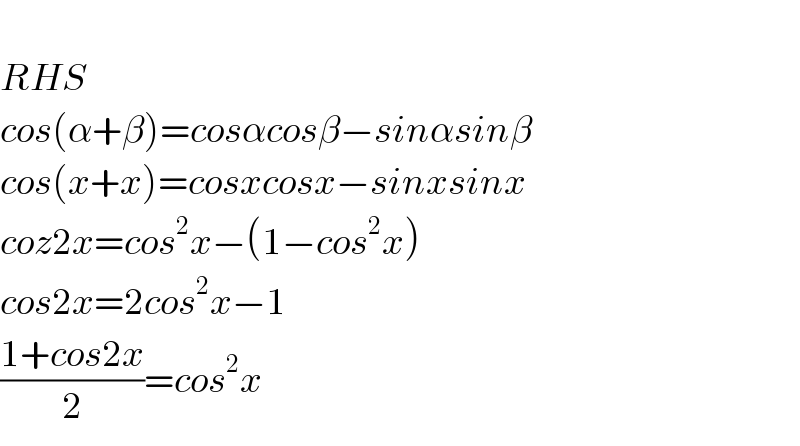
RHS cos(α+β)=cosαcosβ−sinαsinβ cos(x+x)=cosxcosx−sinxsinx coz2x=cos^2 x−(1−cos^2 x) cos2x=2cos^2 x−1 ((1+cos2x)/2)=cos^2 x
$$ \\ $$$${RHS} \\ $$$${cos}\left(\alpha+\beta\right)={cos}\alpha{cos}\beta−{sin}\alpha{sin}\beta \\ $$$${cos}\left({x}+{x}\right)={cosxcosx}−{sinxsinx} \\ $$$${coz}\mathrm{2}{x}={cos}^{\mathrm{2}} {x}−\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right) \\ $$$${cos}\mathrm{2}{x}=\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1} \\ $$$$\frac{\mathrm{1}+{cos}\mathrm{2}{x}}{\mathrm{2}}={cos}^{\mathrm{2}} {x} \\ $$
Answered by $@ty@m last updated on 20/Sep/18
We have cos (a+b)=cos a.cos b−sin a.sin b Put a=b=x cos 2x=cos^2 x−sin^2 x =cos^2 x−(1−cos ^2 x) =2cos^2 x−1 ⇒2cos^2 x=1+cos 2x
$${We}\:{have} \\ $$$$\mathrm{cos}\:\left({a}+{b}\right)=\mathrm{cos}\:{a}.\mathrm{cos}\:{b}−\mathrm{sin}\:{a}.\mathrm{sin}\:{b} \\ $$$${Put}\:{a}={b}={x} \\ $$$$\mathrm{cos}\:\mathrm{2}{x}=\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\:^{\mathrm{2}} {x}−\left(\mathrm{1}−\mathrm{cos}\:\:^{\mathrm{2}} {x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2cos}\:^{\mathrm{2}} {x}=\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *