Question Number 44035 by rahul 19 last updated on 20/Sep/18
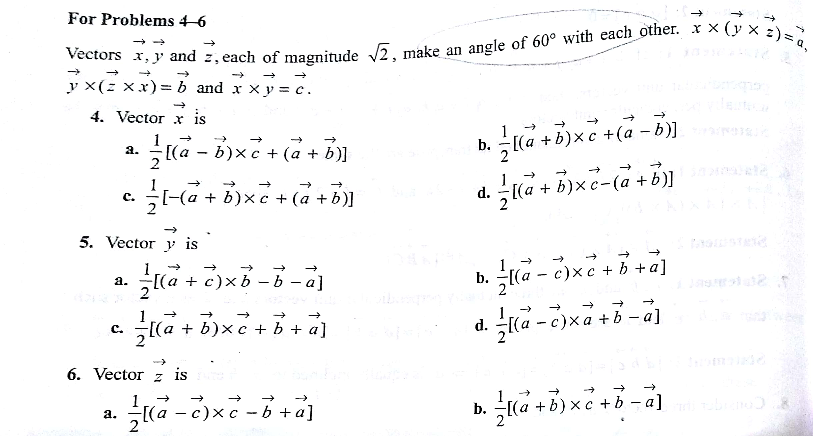
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Sep/18
![(x^→ .z^→ )y^→ −(x^→ .y^→ )z^→ =a^→ ((√2) ×(√2) cos60^o )y^→ −((√2) ×(√2) cos60^o )z^→ =a^→ y^→ −z^→ =a^→ z^→ −x^→ =b^→ x^→ ×y^→ =c^→ (a^→ +b^→ )×c^→ =(y^→ −x^→ )×(x^→ ×y^→ ) =y^→ ×(x^→ ×y^→ )−x^→ ×(x^→ ×y^→ ) =(y^→ .y^→ )x^→ −(y^→ .x^→ )y^→ −(x^→ .y^→ )x^→ +(x^→ .x^→ )y^→ =2x^→ −y^→ −x^→ +2y^→ =x^→ +y^→ x^→ +y^→ =(a^→ +b^→ )×c^→ y^→ −x^→ =a^→ +b^→ 2x^→ =[(a^→ +b^→ )×c^→ −(a^→ +b^→ )] x^→ =(1/2)[(a^→ +b^→ )×c^→ −(a^→ +b^→ )] (a^→ +b^→ )×c^→ +(a^→ +b^→ )=x^→ +y^→ +y^→ −x^→ y^→ =(1/2)[(a^→ +b^→ )×c^→ +(a^→ +b^→ )] (a^→ +b^→ )×c^→ +b^→ −a^→ =x^→ +y^→ +z^→ −x^→ −(y^→ −z^→ ) =x^→ +y^→ +z^→ −x^→ −y^→ +z^→ =2z^→ z^→ =(1/2)[(a^→ +b^→ )×c^→ +b^→ −a^→ )](https://www.tinkutara.com/question/Q44048.png)
$$\left(\overset{\rightarrow} {{x}}.\overset{\rightarrow} {{z}}\right)\overset{\rightarrow} {{y}}−\left(\overset{\rightarrow} {{x}}.\overset{\rightarrow} {{y}}\right)\overset{\rightarrow} {{z}}=\overset{\rightarrow} {{a}} \\ $$$$\left(\sqrt{\mathrm{2}}\:×\sqrt{\mathrm{2}}\:{cos}\mathrm{60}^{{o}} \right)\overset{\rightarrow} {{y}}−\left(\sqrt{\mathrm{2}}\:×\sqrt{\mathrm{2}}\:{cos}\mathrm{60}^{{o}} \right)\overset{\rightarrow} {{z}}=\overset{\rightarrow} {{a}} \\ $$$$\overset{\rightarrow} {{y}}−\overset{\rightarrow} {{z}}=\overset{\rightarrow} {{a}} \\ $$$$\overset{\rightarrow} {{z}}−\overset{\rightarrow} {{x}}=\overset{\rightarrow} {{b}} \\ $$$$\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{y}}=\overset{\rightarrow} {{c}} \\ $$$$\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}}=\left(\overset{\rightarrow} {{y}}−\overset{\rightarrow} {{x}}\right)×\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{y}}\right) \\ $$$$=\overset{\rightarrow} {{y}}×\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{y}}\right)−\overset{\rightarrow} {{x}}×\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{y}}\right) \\ $$$$=\left(\overset{\rightarrow} {{y}}.\overset{\rightarrow} {{y}}\right)\overset{\rightarrow} {{x}}−\left(\overset{\rightarrow} {{y}}.\overset{\rightarrow} {{x}}\right)\overset{\rightarrow} {{y}}−\left(\overset{\rightarrow} {{x}}.\overset{\rightarrow} {{y}}\right)\overset{\rightarrow} {{x}}+\left(\overset{\rightarrow} {{x}}.\overset{\rightarrow} {{x}}\right)\overset{\rightarrow} {{y}} \\ $$$$=\mathrm{2}\overset{\rightarrow} {{x}}−\overset{\rightarrow} {{y}}−\overset{\rightarrow} {{x}}+\mathrm{2}\overset{\rightarrow} {{y}} \\ $$$$=\overset{\rightarrow} {{x}}+\overset{\rightarrow} {{y}} \\ $$$$\overset{\rightarrow} {{x}}+\overset{\rightarrow} {{y}}=\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}} \\ $$$$\overset{\rightarrow} {{y}}−\overset{\rightarrow} {{x}}=\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}} \\ $$$$\mathrm{2}\overset{\rightarrow} {{x}}=\left[\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}}−\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)\right] \\ $$$$\overset{\rightarrow} {{x}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}}−\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)\right] \\ $$$$\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}}+\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)=\overset{\rightarrow} {{x}}+\overset{\rightarrow} {{y}}+\overset{\rightarrow} {{y}}−\overset{\rightarrow} {{x}} \\ $$$$\overset{\rightarrow} {{y}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}}+\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)\right] \\ $$$$\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{a}} \\ $$$$=\overset{\rightarrow} {{x}}+\overset{\rightarrow} {{y}}+\overset{\rightarrow} {{z}}−\overset{\rightarrow} {{x}}−\left(\overset{\rightarrow} {{y}}−\overset{\rightarrow} {{z}}\right) \\ $$$$=\overset{\rightarrow} {{x}}+\overset{\rightarrow} {{y}}+\overset{\rightarrow} {{z}}−\overset{\rightarrow} {{x}}−\overset{\rightarrow} {{y}}+\overset{\rightarrow} {{z}} \\ $$$$=\mathrm{2}\overset{\rightarrow} {{z}} \\ $$$$\overset{\rightarrow} {{z}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{a}}\right) \\ $$
Commented by rahul 19 last updated on 21/Sep/18
Thank you Sir ! ����
Commented by Micky24 last updated on 09/Dec/18

$${pls}\:{how} \\ $$
