Question Number 44094 by peter frank last updated on 21/Sep/18

Commented by tanmay.chaudhury50@gmail.com last updated on 22/Sep/18
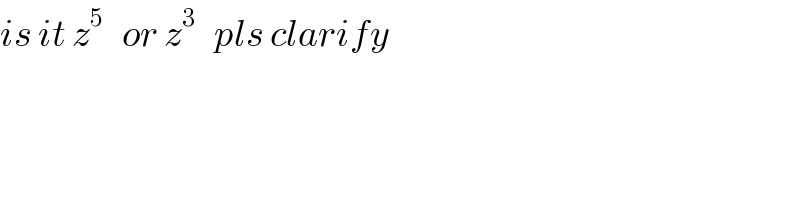
$${is}\:{it}\:{z}^{\mathrm{5}} \:\:\:{or}\:{z}^{\mathrm{3}} \:\:\:{pls}\:{clarify} \\ $$
Commented by peter frank last updated on 23/Sep/18

$${z}^{\mathrm{5}} \: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Sep/18
![a)((x+i(x−2))/(3+i))+((2y+i(1−3y))/(3−i))=i [(3−i){x+i(x−2)}+(3+i){2y+i(1−3y)}]/10=i ((3x+i(3x−6)−ix+(x−2)+6y+i(3−9y)+i2y−(1−3y))/(10))=i ((4x−2+6y−1+3y)/(10))+i((3x−6−x+3−9y+2y)/(10))=i ((4x+9y−3)/(10))+i((2x−7y−3)/(10))=i 4x+9y−3=0 2x−7y−3=10 4x+9y−3=0 4x−14y−26=0 23y+23=0 y=−1 4x−9−3=0 x=3](https://www.tinkutara.com/question/Q44119.png)
$$\left.{a}\right)\frac{{x}+{i}\left({x}−\mathrm{2}\right)}{\mathrm{3}+{i}}+\frac{\mathrm{2}{y}+{i}\left(\mathrm{1}−\mathrm{3}{y}\right)}{\mathrm{3}−{i}}={i} \\ $$$$\left[\left(\mathrm{3}−{i}\right)\left\{{x}+{i}\left({x}−\mathrm{2}\right)\right\}+\left(\mathrm{3}+{i}\right)\left\{\mathrm{2}{y}+{i}\left(\mathrm{1}−\mathrm{3}{y}\right)\right\}\right]/\mathrm{10}={i} \\ $$$$\frac{\mathrm{3}{x}+{i}\left(\mathrm{3}{x}−\mathrm{6}\right)−{ix}+\left({x}−\mathrm{2}\right)+\mathrm{6}{y}+{i}\left(\mathrm{3}−\mathrm{9}{y}\right)+{i}\mathrm{2}{y}−\left(\mathrm{1}−\mathrm{3}{y}\right)}{\mathrm{10}}={i} \\ $$$$\frac{\mathrm{4}{x}−\mathrm{2}+\mathrm{6}{y}−\mathrm{1}+\mathrm{3}{y}}{\mathrm{10}}+{i}\frac{\mathrm{3}{x}−\mathrm{6}−{x}+\mathrm{3}−\mathrm{9}{y}+\mathrm{2}{y}}{\mathrm{10}}={i} \\ $$$$\frac{\mathrm{4}{x}+\mathrm{9}{y}−\mathrm{3}}{\mathrm{10}}+{i}\frac{\mathrm{2}{x}−\mathrm{7}{y}−\mathrm{3}}{\mathrm{10}}={i} \\ $$$$\mathrm{4}{x}+\mathrm{9}{y}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{2}{x}−\mathrm{7}{y}−\mathrm{3}=\mathrm{10} \\ $$$$\mathrm{4}{x}+\mathrm{9}{y}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{4}{x}−\mathrm{14}{y}−\mathrm{26}=\mathrm{0} \\ $$$$\mathrm{23}{y}+\mathrm{23}=\mathrm{0}\:\:\:{y}=−\mathrm{1} \\ $$$$\mathrm{4}{x}−\mathrm{9}−\mathrm{3}=\mathrm{0}\:\:\:\:{x}=\mathrm{3} \\ $$
Commented by peter frank last updated on 21/Sep/18

$${thanks} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Sep/18
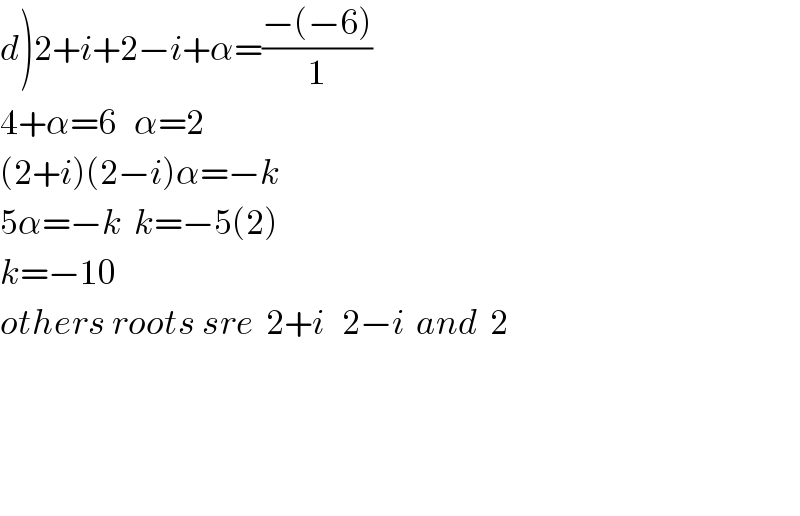
$$\left.{d}\right)\mathrm{2}+{i}+\mathrm{2}−{i}+\alpha=\frac{−\left(−\mathrm{6}\right)}{\mathrm{1}} \\ $$$$\mathrm{4}+\alpha=\mathrm{6}\:\:\:\alpha=\mathrm{2} \\ $$$$\left(\mathrm{2}+{i}\right)\left(\mathrm{2}−{i}\right)\alpha=−{k} \\ $$$$\mathrm{5}\alpha=−{k}\:\:{k}=−\mathrm{5}\left(\mathrm{2}\right) \\ $$$${k}=−\mathrm{10} \\ $$$${others}\:{roots}\:{sre}\:\:\mathrm{2}+{i}\:\:\:\mathrm{2}−{i}\:\:{and}\:\:\mathrm{2} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
