Question Number 23 by user1 last updated on 25/Jan/15
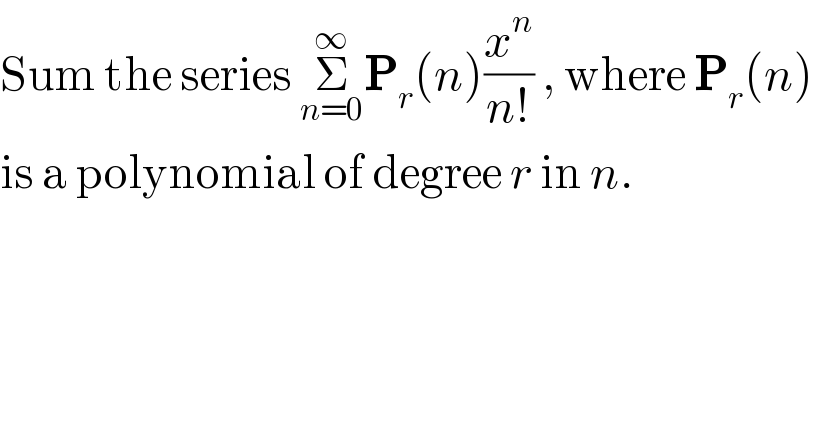
$$\mathrm{Sum}\:\mathrm{the}\:\mathrm{series}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\boldsymbol{\mathrm{P}}_{{r}} \left({n}\right)\frac{{x}^{{n}} }{{n}!}\:,\:\mathrm{where}\:\boldsymbol{\mathrm{P}}_{{r}} \left({n}\right)\: \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{of}\:\mathrm{degree}\:{r}\:\mathrm{in}\:{n}. \\ $$
Answered by user1 last updated on 31/Oct/14
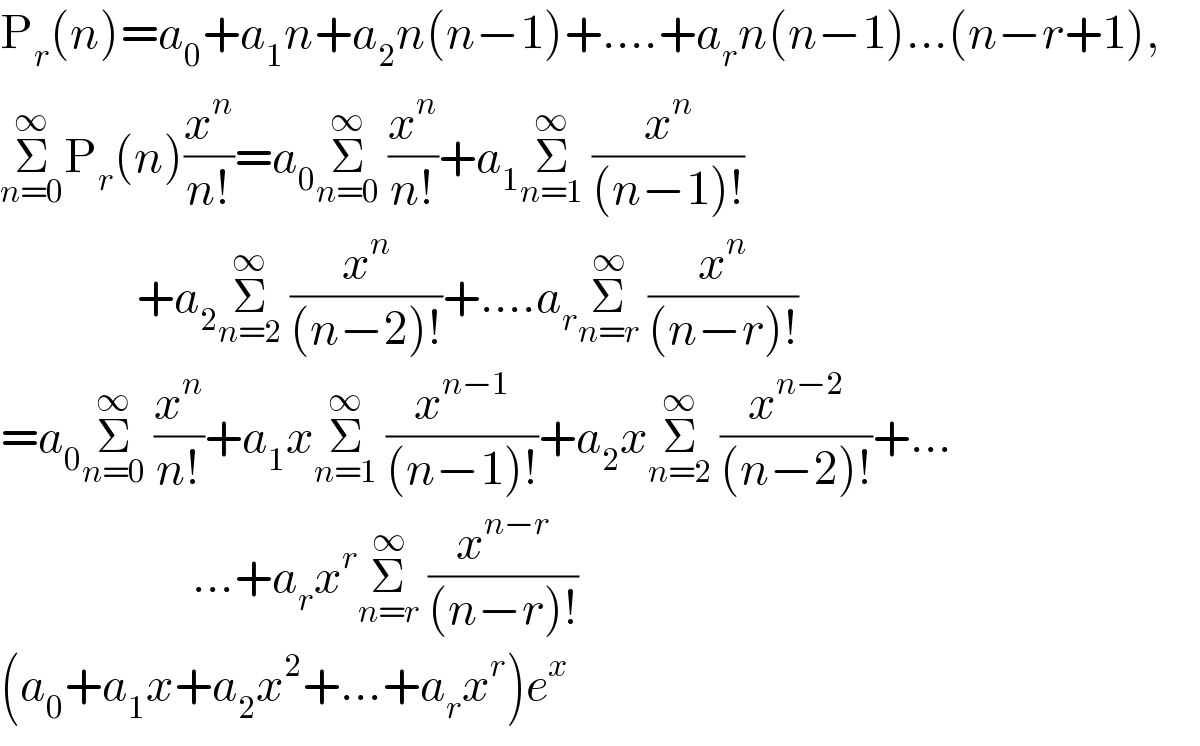
$$\mathrm{P}_{{r}} \left({n}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {n}+{a}_{\mathrm{2}} {n}\left({n}−\mathrm{1}\right)+….+{a}_{{r}} {n}\left({n}−\mathrm{1}\right)…\left({n}−{r}+\mathrm{1}\right),\:\:\:\:\: \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{P}_{{r}} \left({n}\right)\frac{{x}^{{n}} }{{n}!}={a}_{\mathrm{0}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}} }{{n}!}+{a}_{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}} }{\left({n}−\mathrm{1}\right)!} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{a}_{\mathrm{2}} \underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}} }{\left({n}−\mathrm{2}\right)!}+….{a}_{{r}} \underset{{n}={r}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}} }{\left({n}−{r}\right)!} \\ $$$$={a}_{\mathrm{0}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}} }{{n}!}+{a}_{\mathrm{1}} {x}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}−\mathrm{1}} }{\left({n}−\mathrm{1}\right)!}+{a}_{\mathrm{2}} {x}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}−\mathrm{2}} }{\left({n}−\mathrm{2}\right)!}+… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…+{a}_{{r}} {x}^{{r}} \underset{{n}={r}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}−{r}} }{\left({n}−{r}\right)!} \\ $$$$\left({a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +…+{a}_{{r}} {x}^{{r}} \right){e}^{{x}} \\ $$
