Menu Close

Question-44097

Tinku Tara 0 Comments
Pin




Question Number 44097 by peter frank last updated on 21/Sep/18
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Sep/18
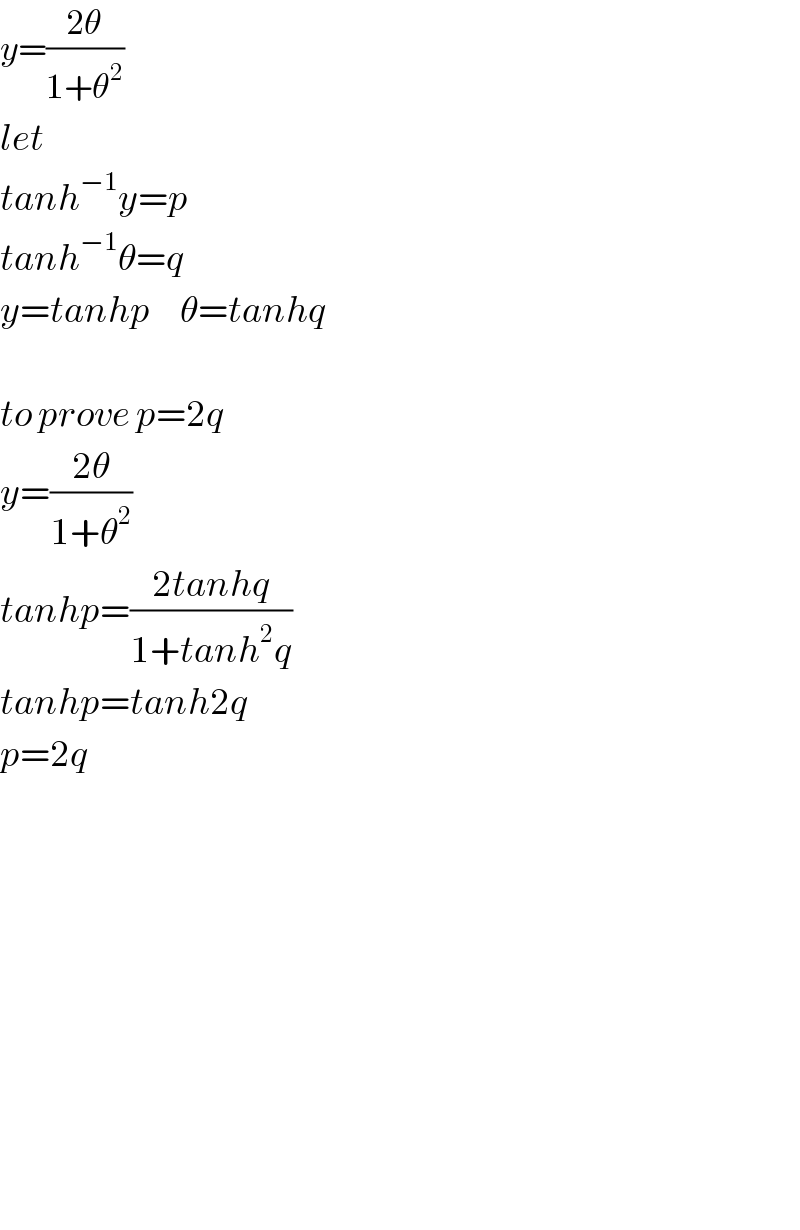
y=((2θ)/(1+θ^2 )) let tanh^(−1) y=p tanh^(−1) θ=q y=tanhp θ=tanhq to prove p=2q y=((2θ)/(1+θ^2 )) tanhp=((2tanhq)/(1+tanh^2 q)) tanhp=tanh2q p=2q
$${y}=\frac{\mathrm{2}\theta}{\mathrm{1}+\theta^{\mathrm{2}} } \\ $$$${let} \\ $$$${tanh}^{−\mathrm{1}} {y}={p} \\ $$$${tanh}^{−\mathrm{1}} \theta={q} \\ $$$${y}={tanhp}\:\:\:\:\:\theta={tanhq} \\ $$$$ \\ $$$${to}\:{prove}\:{p}=\mathrm{2}{q} \\ $$$${y}=\frac{\mathrm{2}\theta}{\mathrm{1}+\theta^{\mathrm{2}} } \\ $$$${tanhp}=\frac{\mathrm{2}{tanhq}}{\mathrm{1}+{tanh}^{\mathrm{2}} {q}} \\ $$$${tanhp}={tanh}\mathrm{2}{q} \\ $$$${p}=\mathrm{2}{q} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Sep/18
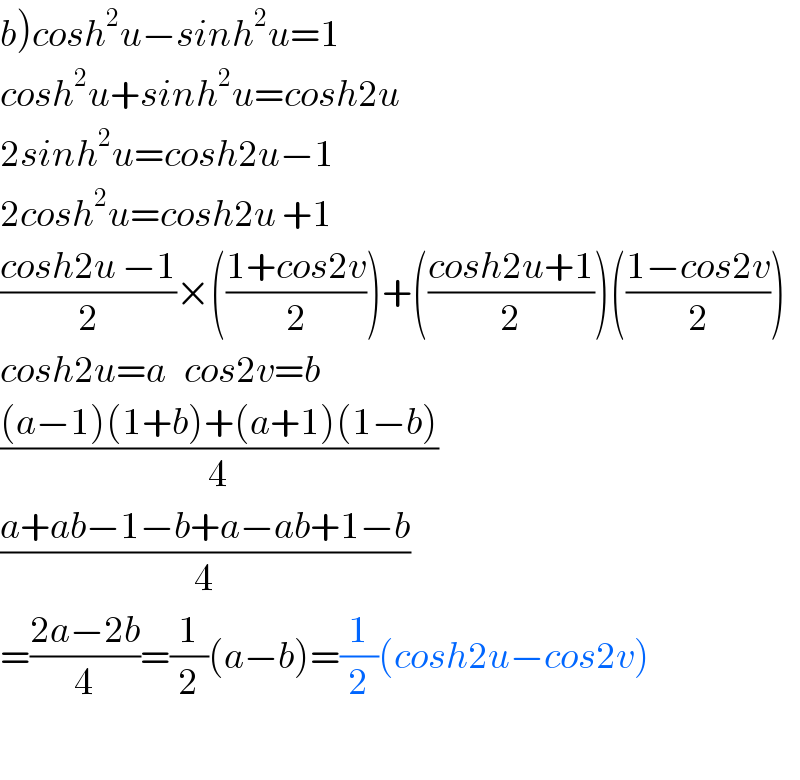
b)cosh^2 u−sinh^2 u=1 cosh^2 u+sinh^2 u=cosh2u 2sinh^2 u=cosh2u−1 2cosh^2 u=cosh2u +1 ((cosh2u −1)/2)×(((1+cos2v)/2))+(((cosh2u+1)/2))(((1−cos2v)/2)) cosh2u=a cos2v=b (((a−1)(1+b)+(a+1)(1−b))/4) ((a+ab−1−b+a−ab+1−b)/4) =((2a−2b)/4)=(1/2)(a−b)=(1/2)(cosh2u−cos2v)
$$\left.{b}\right){cosh}^{\mathrm{2}} {u}−{sinh}^{\mathrm{2}} {u}=\mathrm{1} \\ $$$${cosh}^{\mathrm{2}} {u}+{sinh}^{\mathrm{2}} {u}={cosh}\mathrm{2}{u} \\ $$$$\mathrm{2}{sinh}^{\mathrm{2}} {u}={cosh}\mathrm{2}{u}−\mathrm{1} \\ $$$$\mathrm{2}{cosh}^{\mathrm{2}} {u}={cosh}\mathrm{2}{u}\:+\mathrm{1} \\ $$$$\frac{{cosh}\mathrm{2}{u}\:−\mathrm{1}}{\mathrm{2}}×\left(\frac{\mathrm{1}+{cos}\mathrm{2}{v}}{\mathrm{2}}\right)+\left(\frac{{cosh}\mathrm{2}{u}+\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}−{cos}\mathrm{2}{v}}{\mathrm{2}}\right) \\ $$$${cosh}\mathrm{2}{u}={a}\:\:\:{cos}\mathrm{2}{v}={b} \\ $$$$\frac{\left({a}−\mathrm{1}\right)\left(\mathrm{1}+{b}\right)+\left({a}+\mathrm{1}\right)\left(\mathrm{1}−{b}\right)}{\mathrm{4}} \\ $$$$\frac{{a}+{ab}−\mathrm{1}−{b}+{a}−{ab}+\mathrm{1}−{b}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{2}{a}−\mathrm{2}{b}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}−{b}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({cosh}\mathrm{2}{u}−{cos}\mathrm{2}{v}\right) \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Sep/18
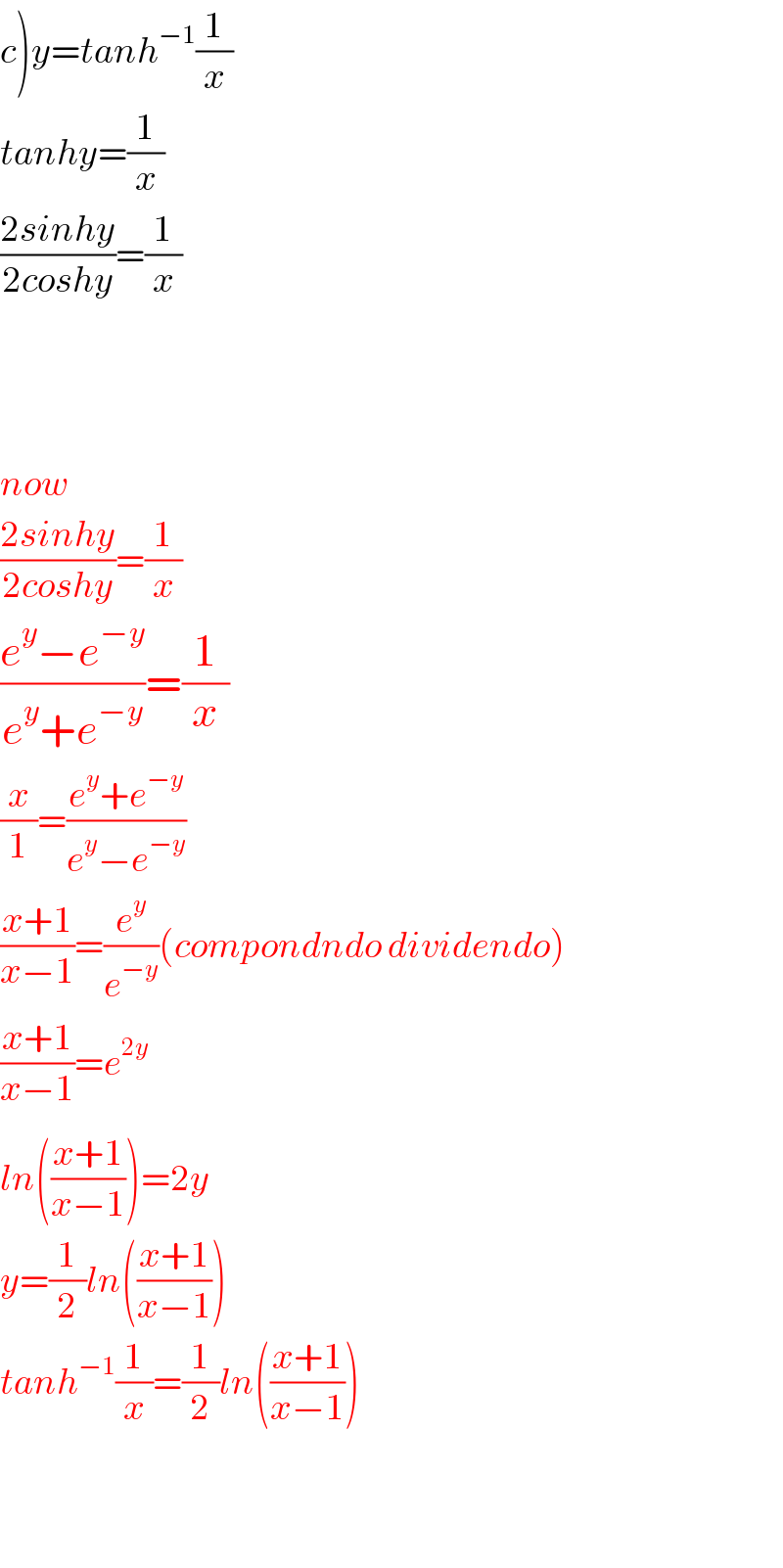
c)y=tanh^(−1) (1/x) tanhy=(1/x) ((2sinhy)/(2coshy))=(1/x) now ((2sinhy)/(2coshy))=(1/x) ((e^y −e^(−y) )/(e^y +e^(−y) ))=(1/x) (x/1)=((e^y +e^(−y) )/(e^y −e^(−y) )) ((x+1)/(x−1))=(e^y /e^(−y) )(compondndo dividendo) ((x+1)/(x−1))=e^(2y) ln(((x+1)/(x−1)))^ =2y y=(1/2)ln(((x+1)/(x−1))) tanh^(−1) (1/x)=(1/2)ln(((x+1)/(x−1)))
$$\left.{c}\right){y}={tanh}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}} \\ $$$${tanhy}=\frac{\mathrm{1}}{{x}} \\ $$$$\frac{\mathrm{2}{sinhy}}{\mathrm{2}{coshy}}=\frac{\mathrm{1}}{{x}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${now} \\ $$$$\frac{\mathrm{2}{sinhy}}{\mathrm{2}{coshy}}=\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{e}^{{y}} −{e}^{−{y}} }{{e}^{{y}} +{e}^{−{y}} }=\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{x}}{\mathrm{1}}=\frac{{e}^{{y}} +{e}^{−{y}} }{{e}^{{y}} −{e}^{−{y}} } \\ $$$$\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}=\frac{{e}^{{y}} }{{e}^{−{y}} }\left({compondndo}\:{dividendo}\right) \\ $$$$\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}={e}^{\mathrm{2}{y}} \\ $$$${ln}\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\overset{} {\right)}=\mathrm{2}{y} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$$${tanh}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *