Question Number 109721 by Algoritm last updated on 25/Aug/20
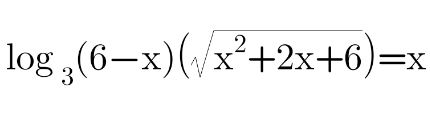
Answered by 1549442205PVT last updated on 25/Aug/20
![We need have the condition that 6−x>0 for logarithm is meaning.Then log_3 (6−x)(√(x^2 +2x+6))=x ⇔log_3 (6−x)(√(x^2 +2x+6)) −x=0 Put f(x)=(6−x)(√(x^2 +2x+6)) −x f ′(x)=(1/((ln3)(6−x)(√(x^2 +2x+6)) ))×[(6−x)(√(x^2 +2x+6)) ]′−1 ={(1/(ln3(6−x)(√(x^2 +2x+6)) ))×[(6−x).((x+1)/()(√(x^2 +2x+6)) ))−(√(x^2 +2x+6)) ]}−1 ={(1/(ln3(6−x)(√(x^2 +2x+6)) ))×((−x^2 +5x+6−(x^2 +2x+6))/( (√(x^2 +2x+6))))}−1 ={(1/(ln3(6−x)(√(x^2 +2x+6)) ))×((−2x^2 +3x)/( (√(x^2 +2x+6))))}−1 =((−2x^2 +3x)/(ln3(6−x)(x^2 +2x+6)))−1 we prove that f ′(x)<0 ∀x<6.Indeed, f ′(x)<0⇔((−2x^2 +3x)/(ln3(6−x)(x^2 +2x+6)))−1<0 ⇔ln3(6−x)(x^2 +2x+6)>−2x^2 +3x Since ln3>1,it is enough to prove that (6−x)(x^2 +2x+6)>−2x^2 +3x (∗) ⇔−x^3 +4x^2 +6x+36>−2x^2 +3x ⇔−x^3 +6x+3x+36>0 Put h(x)=−x^3 +6x^2 +3x+36 h′(x)=−3x^2 +12x+3=0 ⇔−x^2 +4x+1=0 Δ′=4+1=5 x_(1,2) =2±(√5) .We have variable tablet determinant (((−∞),,(2−(√5)),,,(2+(√5)),,,6),((h′(x)),(−↘),,,+,,↘,−,),((h(x)),,(35.64),↗,,(80.36),,,(54))) From above tablet we have :h(6)=54 h_(min) (x)=35.6,h_(max) (x)=80.3,x∈(−∞;6) .This shows that h(x)>0∀x<6 Hence the inequality(∗) is true ∀x<6 which means f ′(x)<0∀x<6 ,so we infer f(x)is decreasing function that means the equation f(x)=0 has no more one roots.Solve the f(x)=0 ⇔log_3 (6−x)(√(x^2 +2x+6)) −x=0 we get the root x=2.440710525 Thus the give eqution has unique root x=2.440710525](https://www.tinkutara.com/question/Q109740.png)
$$\mathrm{We}\:\mathrm{need}\:\mathrm{have}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{that} \\ $$$$\mathrm{6}−\mathrm{x}>\mathrm{0}\:\mathrm{for}\:\mathrm{logarithm}\:\mathrm{is}\:\mathrm{meaning}.\mathrm{Then} \\ $$$$\mathrm{log}_{\mathrm{3}} \left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}=\mathrm{x} \\ $$$$\Leftrightarrow\mathrm{log}_{\mathrm{3}} \left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:−\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{Put}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:−\mathrm{x} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{ln3}\right)\left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:}×\left[\left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:\right]'−\mathrm{1} \\ $$$$=\left\{\frac{\mathrm{1}}{\mathrm{ln3}\left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:}×\left[\left(\mathrm{6}−\mathrm{x}\right).\frac{\mathrm{x}+\mathrm{1}}{\left.\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:\right]\right\}−\mathrm{1} \\ $$$$=\left\{\frac{\mathrm{1}}{\mathrm{ln3}\left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:}×\frac{−\mathrm{x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{6}−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}\right)}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}}\right\}−\mathrm{1} \\ $$$$=\left\{\frac{\mathrm{1}}{\mathrm{ln3}\left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:}×\frac{−\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}}\right\}−\mathrm{1} \\ $$$$=\frac{−\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}}{\mathrm{ln3}\left(\mathrm{6}−\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}\right)}−\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{f}\:'\left(\mathrm{x}\right)<\mathrm{0}\:\:\:\forall\mathrm{x}<\mathrm{6}.\mathrm{Indeed}, \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)<\mathrm{0}\Leftrightarrow\frac{−\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}}{\mathrm{ln3}\left(\mathrm{6}−\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}\right)}−\mathrm{1}<\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{ln3}\left(\mathrm{6}−\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}\right)>−\mathrm{2x}^{\mathrm{2}} +\mathrm{3x} \\ $$$$\mathrm{Since}\:\mathrm{ln3}>\mathrm{1},\mathrm{it}\:\mathrm{is}\:\mathrm{enough}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\left(\mathrm{6}−\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}\right)>−\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}\:\:\left(\ast\right) \\ $$$$\Leftrightarrow−\mathrm{x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{36}>−\mathrm{2x}^{\mathrm{2}} +\mathrm{3x} \\ $$$$\Leftrightarrow−\mathrm{x}^{\mathrm{3}} +\mathrm{6x}+\mathrm{3x}+\mathrm{36}>\mathrm{0} \\ $$$$\mathrm{Put}\:\mathrm{h}\left(\mathrm{x}\right)=−\mathrm{x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{36} \\ $$$$\mathrm{h}'\left(\mathrm{x}\right)=−\mathrm{3x}^{\mathrm{2}} +\mathrm{12x}+\mathrm{3}=\mathrm{0} \\ $$$$\Leftrightarrow−\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{1}=\mathrm{0}\:\Delta'=\mathrm{4}+\mathrm{1}=\mathrm{5} \\ $$$$\mathrm{x}_{\mathrm{1},\mathrm{2}} =\mathrm{2}\pm\sqrt{\mathrm{5}}\:.\mathrm{We}\:\mathrm{have}\:\mathrm{variable}\:\mathrm{tablet} \\ $$$$\begin{vmatrix}{−\infty}&{}&{\mathrm{2}−\sqrt{\mathrm{5}}}&{}&{}&{\mathrm{2}+\sqrt{\mathrm{5}}}&{}&{}&{\mathrm{6}}\\{\mathrm{h}'\left(\mathrm{x}\right)}&{−\searrow}&{}&{}&{+}&{}&{\searrow}&{−}&{}\\{\mathrm{h}\left(\mathrm{x}\right)}&{}&{\mathrm{35}.\mathrm{64}}&{\nearrow}&{}&{\mathrm{80}.\mathrm{36}}&{}&{}&{\mathrm{54}}\end{vmatrix} \\ $$$$\mathrm{From}\:\mathrm{above}\:\mathrm{tablet}\:\mathrm{we}\:\mathrm{have}\::\mathrm{h}\left(\mathrm{6}\right)=\mathrm{54} \\ $$$$\mathrm{h}_{\mathrm{min}} \left(\mathrm{x}\right)=\mathrm{35}.\mathrm{6},\mathrm{h}_{\mathrm{max}} \left(\mathrm{x}\right)=\mathrm{80}.\mathrm{3},\mathrm{x}\in\left(−\infty;\mathrm{6}\right) \\ $$$$.\mathrm{This}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{h}\left(\mathrm{x}\right)>\mathrm{0}\forall\mathrm{x}<\mathrm{6} \\ $$$$\mathrm{Hence}\:\mathrm{the}\:\mathrm{inequality}\left(\ast\right)\:\mathrm{is}\:\mathrm{true}\:\forall\mathrm{x}<\mathrm{6} \\ $$$$\mathrm{which}\:\mathrm{means}\:\mathrm{f}\:'\left(\mathrm{x}\right)<\mathrm{0}\forall\mathrm{x}<\mathrm{6}\:,\mathrm{so}\:\mathrm{we}\:\mathrm{infer} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\mathrm{is}\:\mathrm{decreasing}\:\mathrm{function}\:\mathrm{that}\:\mathrm{means} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\:\mathrm{has}\:\mathrm{no}\:\mathrm{more} \\ $$$$\mathrm{one}\:\mathrm{roots}.\mathrm{Solve}\:\mathrm{the}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{log}_{\mathrm{3}} \left(\mathrm{6}−\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{6}}\:−\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{root}\:\:\:\mathrm{x}=\mathrm{2}.\mathrm{440710525} \\ $$$$\mathrm{Thus}\:\mathrm{the}\:\mathrm{give}\:\mathrm{eqution}\:\mathrm{has}\:\mathrm{unique} \\ $$$$\boldsymbol{\mathrm{root}}\:\boldsymbol{\mathrm{x}}=\mathrm{2}.\mathrm{440710525} \\ $$
Commented by Algoritm last updated on 25/Aug/20

$$\mathrm{x}\approx\mathrm{3}.\mathrm{8} \\ $$
Commented by 1549442205PVT last updated on 25/Aug/20
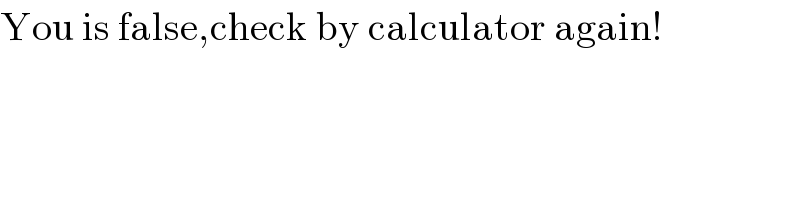
$$\mathrm{You}\:\mathrm{is}\:\mathrm{false},\mathrm{check}\:\mathrm{by}\:\mathrm{calculator}\:\mathrm{again}! \\ $$
Commented by Algoritm last updated on 25/Aug/20
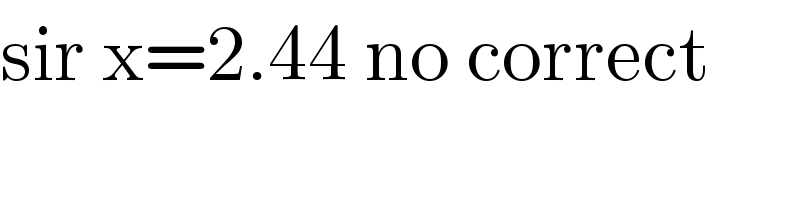
$$\mathrm{sir}\:\mathrm{x}=\mathrm{2}.\mathrm{44}\:\mathrm{no}\:\mathrm{correct} \\ $$
