Question Number 44264 by pramid last updated on 25/Sep/18
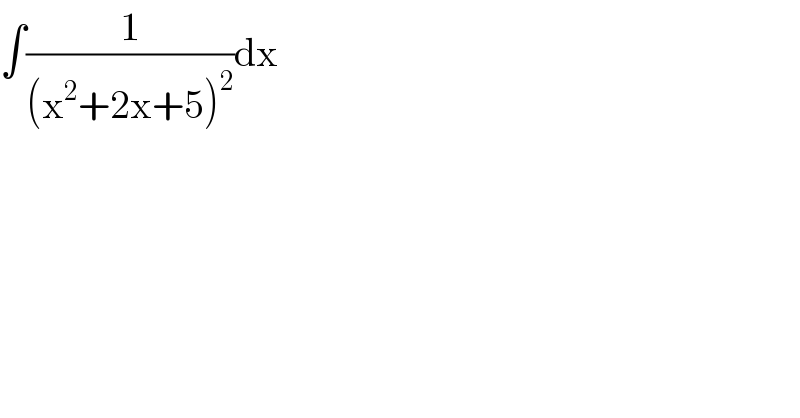
$$\int\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{5}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Commented by maxmathsup by imad last updated on 25/Sep/18
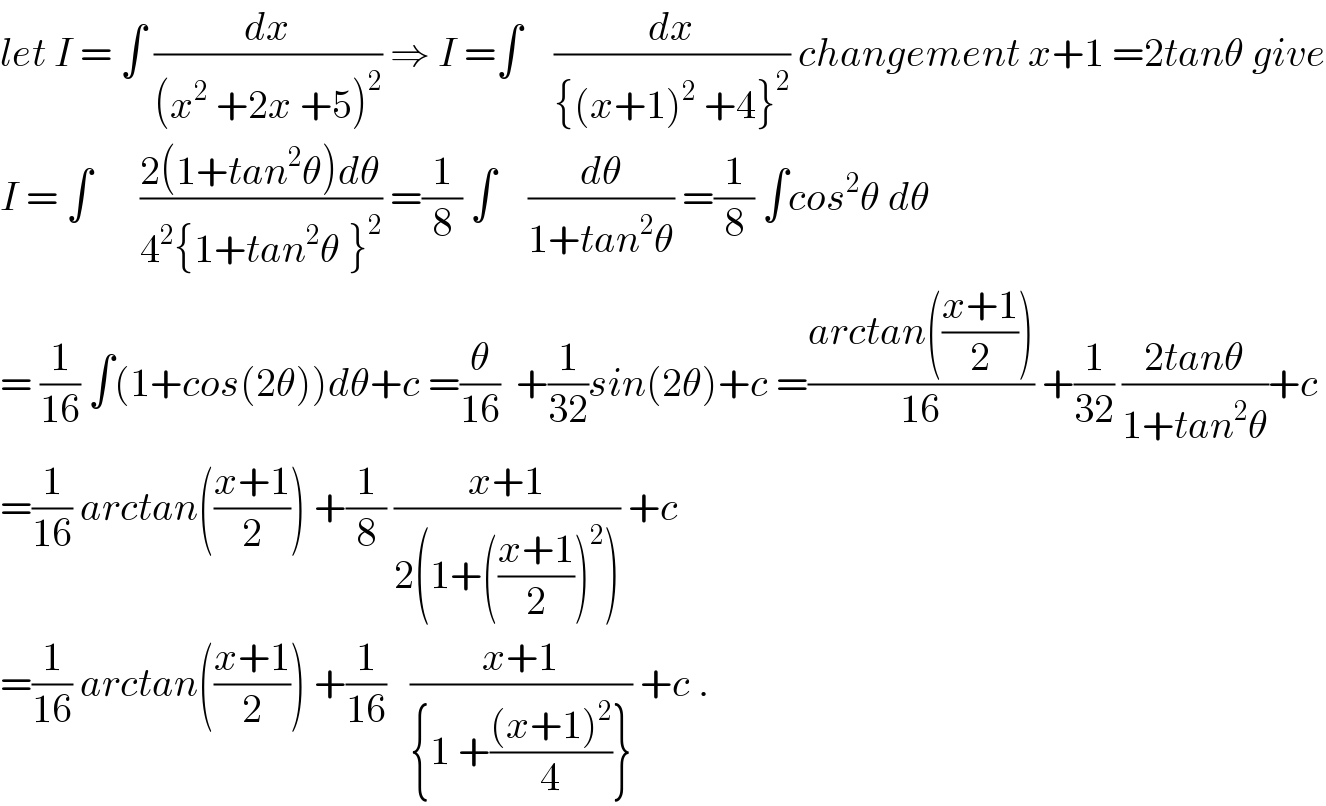
$${let}\:{I}\:=\:\int\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{5}\right)^{\mathrm{2}} }\:\Rightarrow\:{I}\:=\int\:\:\:\:\frac{{dx}}{\left\{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{4}\right\}^{\mathrm{2}} }\:{changement}\:{x}+\mathrm{1}\:=\mathrm{2}{tan}\theta\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\:\:\frac{\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\mathrm{4}^{\mathrm{2}} \left\{\mathrm{1}+{tan}^{\mathrm{2}} \theta\:\right\}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{8}}\:\int\:\:\:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:=\frac{\mathrm{1}}{\mathrm{8}}\:\int{cos}^{\mathrm{2}} \theta\:{d}\theta \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{16}}\:\int\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right){d}\theta+{c}\:=\frac{\theta}{\mathrm{16}}\:\:+\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{2}\theta\right)+{c}\:=\frac{{arctan}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{32}}\:\frac{\mathrm{2}{tan}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:{arctan}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{8}}\:\frac{{x}+\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right)}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:{arctan}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{16}}\:\:\:\frac{{x}+\mathrm{1}}{\left\{\mathrm{1}\:+\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\right\}}\:+{c}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Sep/18
![∫(dx/({(x+1)^2 +2^2 }^2 )) x+1=2tanα dx=2sec^2 αdα ∫((2sec^2 αdα)/({2^2 tan^2 α+2^2 }^2 )) ∫((2sec^2 αdα)/({2^2 (1+tan^2 α)}^2 )) ∫((2sec^2 αdα)/(2^4 sec^4 α)) (1/8)∫(dα/(sec^2 α)) (1/(16))∫(1+co2α)dα (1/(16))[α+((sin2α)/2)]+c (1/(16))[tan^(−1) (((x+1)/2))+(1/2)×((2tanα)/(1+tan^2 α))] (1/(16))[tan^(−1) (((x+1)/2))+(((x+1)/2)/(1+(((x+1)/2))^2 ))]+c](https://www.tinkutara.com/question/Q44266.png)
$$\int\frac{{dx}}{\left\{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \right\}^{\mathrm{2}} } \\ $$$${x}+\mathrm{1}=\mathrm{2}{tan}\alpha \\ $$$${dx}=\mathrm{2}{sec}^{\mathrm{2}} \alpha{d}\alpha \\ $$$$\int\frac{\mathrm{2}{sec}^{\mathrm{2}} \alpha{d}\alpha}{\left\{\mathrm{2}^{\mathrm{2}} {tan}^{\mathrm{2}} \alpha+\mathrm{2}^{\mathrm{2}} \right\}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{2}{sec}^{\mathrm{2}} \alpha{d}\alpha}{\left\{\mathrm{2}^{\mathrm{2}} \left(\mathrm{1}+{tan}^{\mathrm{2}} \alpha\right)\right\}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{2}{sec}^{\mathrm{2}} \alpha{d}\alpha}{\mathrm{2}^{\mathrm{4}} {sec}^{\mathrm{4}} \alpha} \\ $$$$\frac{\mathrm{1}}{\mathrm{8}}\int\frac{{d}\alpha}{{sec}^{\mathrm{2}} \alpha} \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\int\left(\mathrm{1}+{co}\mathrm{2}\alpha\right){d}\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\left[\alpha+\frac{{sin}\mathrm{2}\alpha}{\mathrm{2}}\right]+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\left[{tan}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{tan}\alpha}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\left[{tan}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)+\frac{\frac{{x}+\mathrm{1}}{\mathrm{2}}}{\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\right]+{c} \\ $$$$ \\ $$
