Menu Close

Question-109855

Tinku Tara 0 Comments
Pin




Question Number 109855 by aurpeyz last updated on 26/Aug/20
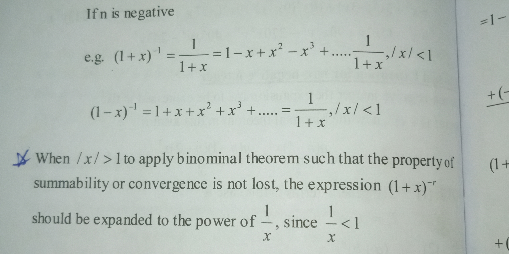
Answered by aurpeyz last updated on 26/Aug/20
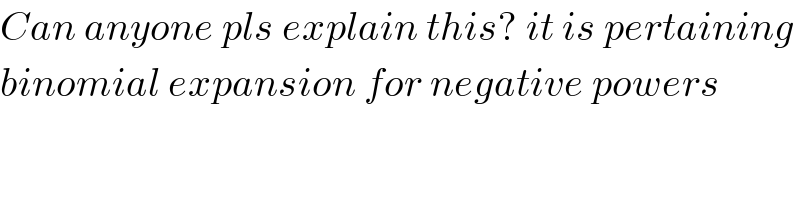
Can anyone pls explain this? it is pertaining binomial expansion for negative powers
$${Can}\:{anyone}\:{pls}\:{explain}\:{this}?\:{it}\:{is}\:{pertaining} \\ $$$${binomial}\:{expansion}\:{for}\:{negative}\:{powers} \\ $$
Commented by mathdave last updated on 26/Aug/20
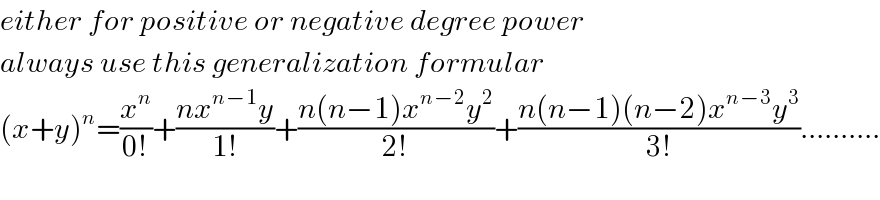
either for positive or negative degree power always use this generalization formular (x+y)^n =(x^n /(0!))+((nx^(n−1) y)/(1!))+((n(n−1)x^(n−2) y^2 )/(2!))+((n(n−1)(n−2)x^(n−3) y^3 )/(3!))..........
$${either}\:{for}\:{positive}\:{or}\:{negative}\:{degree}\:{power} \\ $$$${always}\:{use}\:{this}\:{generalization}\:{formular} \\ $$$$\left({x}+{y}\right)^{{n}} =\frac{{x}^{{n}} }{\mathrm{0}!}+\frac{{nx}^{{n}−\mathrm{1}} {y}}{\mathrm{1}!}+\frac{{n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} {y}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right){x}^{{n}−\mathrm{3}} {y}^{\mathrm{3}} }{\mathrm{3}!}………. \\ $$
Answered by Her_Majesty last updated on 26/Aug/20
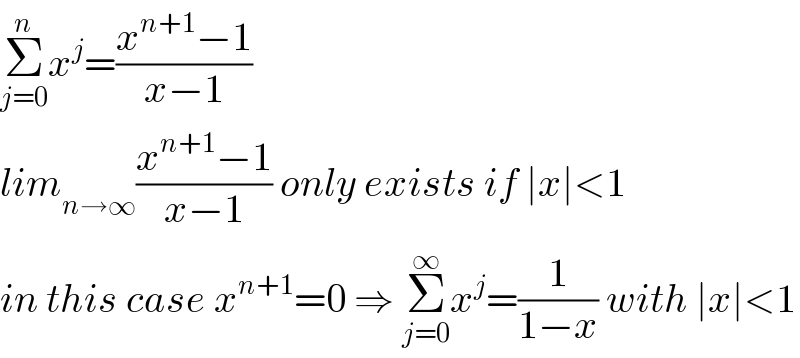
Σ_(j=0) ^n x^j =((x^(n+1) −1)/(x−1)) lim_(n→∞) ((x^(n+1) −1)/(x−1)) only exists if ∣x∣<1 in this case x^(n+1) =0 ⇒ Σ_(j=0) ^∞ x^j =(1/(1−x)) with ∣x∣<1
$$\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{j}} =\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}} \\ $$$${lim}_{{n}\rightarrow\infty} \frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\:{only}\:{exists}\:{if}\:\mid{x}\mid<\mathrm{1} \\ $$$${in}\:{this}\:{case}\:{x}^{{n}+\mathrm{1}} =\mathrm{0}\:\Rightarrow\:\underset{{j}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{j}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$
Answered by Rio Michael last updated on 26/Aug/20
Given the general binomial expansion (1 + x)^n , then general term expressed as a summation is given as (1 + x)^n = Σ_(k =0) ^n ^n C_k x^(n−k) It is known that the series is convergent if ∣x∣ < 1. If we wish to expand such that ∣x∣ > 1, then it must be expanded in terms of (1/x) , this works since (1/x) < 1 and will be carried out for the expansion′s of (1 + x)^(−n) only.
$$\mathrm{Given}\:\mathrm{the}\:\mathrm{general}\:\mathrm{binomial}\:\mathrm{expansion}\:\left(\mathrm{1}\:+\:{x}\right)^{{n}} ,\:\mathrm{then}\:\mathrm{general} \\ $$$$\mathrm{term}\:\mathrm{expressed}\:\mathrm{as}\:\mathrm{a}\:\mathrm{summation}\:\mathrm{is}\:\mathrm{given}\:\mathrm{as} \\ $$$$\left(\mathrm{1}\:+\:{x}\right)^{{n}} \:=\:\underset{{k}\:=\mathrm{0}} {\overset{{n}} {\sum}}\:^{{n}} {C}_{{k}} \:{x}^{{n}−{k}} \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{known}\:\mathrm{that}\:\mathrm{the}\:\mathrm{series}\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{if}\:\mid{x}\mid\:<\:\mathrm{1}. \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{wish}\:\mathrm{to}\:\mathrm{expand}\:\mathrm{such}\:\mathrm{that}\:\mid{x}\mid\:>\:\mathrm{1},\:\mathrm{then}\:\mathrm{it} \\ $$$$\mathrm{must}\:\mathrm{be}\:\mathrm{expanded}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\frac{\mathrm{1}}{{x}}\:,\:\mathrm{this}\:\mathrm{works}\:\mathrm{since}\:\frac{\mathrm{1}}{{x}}\:<\:\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{will}\:\mathrm{be}\:\mathrm{carried}\:\mathrm{out}\:\mathrm{for}\:\mathrm{the}\:\mathrm{expansion}'\mathrm{s}\:\mathrm{of}\:\:\left(\mathrm{1}\:+\:{x}\right)^{−{n}} \:\mathrm{only}. \\ $$
Commented by aurpeyz last updated on 26/Aug/20
pls. What is the implication of this statement? Does that mean that i have to factorize any question on negative power binomial to get the form (1/x) in other to get the right ans
$${pls}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{implication}\:\mathrm{of}\:\mathrm{this}\:\mathrm{statement}? \\ $$$$\mathrm{Does}\:\mathrm{that}\:\mathrm{mean}\:\mathrm{that}\:\mathrm{i}\:\mathrm{have}\:\mathrm{to}\:\mathrm{factorize} \\ $$$$\mathrm{any}\:\mathrm{question}\:\mathrm{on}\:\mathrm{negative}\:\mathrm{power}\:\mathrm{binomial}\:\mathrm{to} \\ $$$$\mathrm{get}\:\mathrm{the}\:\mathrm{form}\:\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{in}\:\mathrm{other}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{right}\:\mathrm{ans} \\ $$
Commented by aurpeyz last updated on 26/Aug/20
That is exactly where I am getting confused. Anytime i have a negative power. I always factorize the binomial to get the form (1/x) in expansion. but the problem is that it doesnt work for all kinds of problem
$$\mathrm{That}\:\mathrm{is}\:\mathrm{exactly}\:\mathrm{where}\:\mathrm{I}\:\mathrm{am}\:\mathrm{getting}\:\mathrm{confused}. \\ $$$$\mathrm{Anytime}\:\mathrm{i}\:\mathrm{have}\:\mathrm{a}\:\mathrm{negative}\:\mathrm{power}.\:\mathrm{I}\:\mathrm{always} \\ $$$$\mathrm{factorize}\:\mathrm{the}\:\mathrm{binomial}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{form}\:\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{in}\: \\ $$$$\mathrm{expansion}.\:\mathrm{but}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{is}\:\mathrm{that}\:\mathrm{it}\:\mathrm{doesnt}\:\mathrm{work} \\ $$$$\mathrm{for}\:\mathrm{all}\:\mathrm{kinds}\:\mathrm{of}\:\mathrm{problem} \\ $$
Commented by Rio Michael last updated on 26/Aug/20
No its expansion as you would for anyother problem. Most at times it will appear in terms of (1/x) , if it doesn′t then either the series doesn′t converge or it′s got a particular range of numbers for which it converges.
$$\:\mathrm{No}\:\mathrm{its}\:\mathrm{expansion}\:\mathrm{as}\:\mathrm{you}\:\mathrm{would}\:\mathrm{for}\:\mathrm{anyother}\:\mathrm{problem}. \\ $$$$\mathrm{Most}\:\mathrm{at}\:\mathrm{times}\:\mathrm{it}\:\mathrm{will}\:\mathrm{appear}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\frac{\mathrm{1}}{{x}}\:,\:\mathrm{if}\:\mathrm{it}\:\mathrm{doesn}'\mathrm{t} \\ $$$$\mathrm{then}\:\mathrm{either}\:\mathrm{the}\:\mathrm{series}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{converge}\:\mathrm{or}\:\mathrm{it}'\mathrm{s}\:\mathrm{got}\:\mathrm{a}\:\mathrm{particular} \\ $$$$\mathrm{range}\:\mathrm{of}\:\mathrm{numbers}\:\mathrm{for}\:\mathrm{which}\:\mathrm{it}\:\mathrm{converges}. \\ $$
Commented by aurpeyz last updated on 27/Aug/20
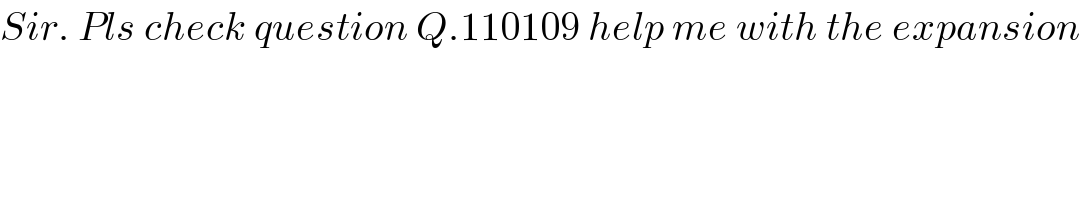
Sir. Pls check question Q.110109 help me with the expansion
$${Sir}.\:{Pls}\:{check}\:{question}\:{Q}.\mathrm{110109}\:{help}\:{me}\:{with}\:{the}\:{expansion} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *