Question-109909

Facebook Tweet Pin

Question Number 109909 by mathdave last updated on 26/Aug/20

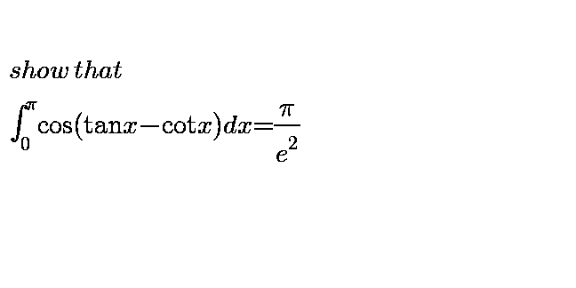
Commented by mnjuly1970 last updated on 26/Aug/20

$${nice}\:{problem}\:{but}\:{a}\:{little}\:{bit} \\ $$$${difficult}.\:\bigstar \\ $$

Commented by mathdave last updated on 26/Aug/20

$${it}\:{very}\:{simple}\:{problem} \\ $$

Commented by mohammad17 last updated on 26/Aug/20

$${sir}\:{i}\:{want}\:{the}\:{solution}\:{this}\:{problem} \\ $$

Commented by mathmax by abdo last updated on 26/Aug/20

if you have seen the answer in a book...

$$\mathrm{if}\:\mathrm{you}\:\mathrm{have}\:\mathrm{seen}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{a}\:\:\mathrm{book}… \\ $$

Commented by mathdave last updated on 26/Aug/20

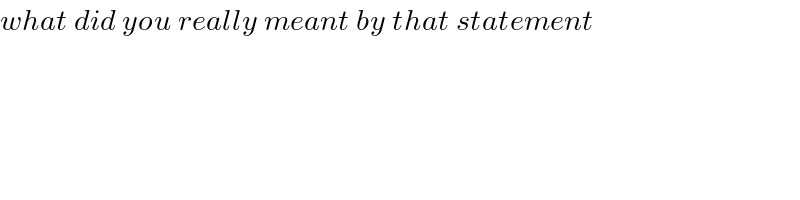
$${what}\:{did}\:{you}\:{really}\:{meant}\:{by}\:{that}\:{statement} \\ $$

Commented by mathmax by abdo last updated on 26/Aug/20

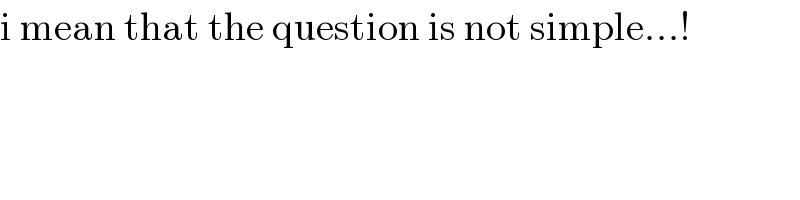
i mean that the question is not simple...!

$$\mathrm{i}\:\mathrm{mean}\:\mathrm{that}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{simple}…! \\ $$

Answered by mnjuly1970 last updated on 26/Aug/20

Answered by mathmax by abdo last updated on 26/Aug/20

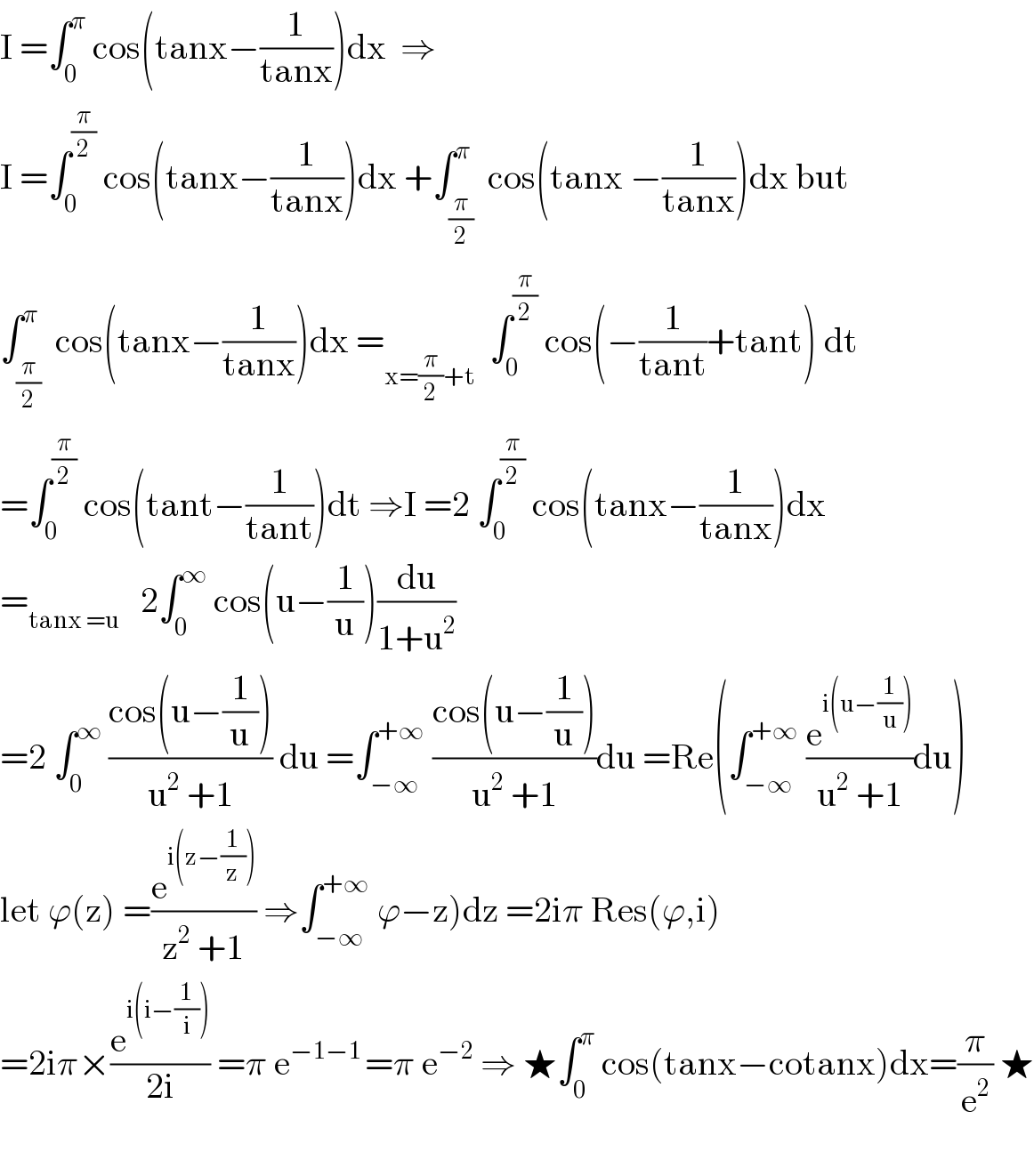
I =∫_0 ^π cos(tanx−(1/(tanx)))dx ⇒ I =∫_0 ^(π/2) cos(tanx−(1/(tanx)))dx +∫_(π/2) ^π cos(tanx −(1/(tanx)))dx but ∫_(π/2) ^π cos(tanx−(1/(tanx)))dx =_(x=(π/2)+t) ∫_0 ^(π/2) cos(−(1/(tant))+tant) dt =∫_0 ^(π/2) cos(tant−(1/(tant)))dt ⇒I =2 ∫_0 ^(π/2) cos(tanx−(1/(tanx)))dx =_(tanx =u) 2∫_0 ^∞ cos(u−(1/u))(du/(1+u^2 )) =2 ∫_0 ^∞ ((cos(u−(1/u)))/(u^2 +1)) du =∫_(−∞) ^(+∞) ((cos(u−(1/u)))/(u^2 +1))du =Re(∫_(−∞) ^(+∞) (e^(i(u−(1/u))) /(u^2 +1))du) let ϕ(z) =(e^(i(z−(1/z))) /(z^2 +1)) ⇒∫_(−∞) ^(+∞) ϕ−z)dz =2iπ Res(ϕ,i) =2iπ×(e^(i(i−(1/i))) /(2i)) =π e^(−1−1 ) =π e^(−2) ⇒ ★∫_0 ^π cos(tanx−cotanx)dx=(π/e^2 ) ★

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}\left(\mathrm{tanx}−\frac{\mathrm{1}}{\mathrm{tanx}}\right)\mathrm{dx}\:\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{tanx}−\frac{\mathrm{1}}{\mathrm{tanx}}\right)\mathrm{dx}\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\mathrm{cos}\left(\mathrm{tanx}\:−\frac{\mathrm{1}}{\mathrm{tanx}}\right)\mathrm{dx}\:\mathrm{but} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\mathrm{cos}\left(\mathrm{tanx}−\frac{\mathrm{1}}{\mathrm{tanx}}\right)\mathrm{dx}\:=_{\mathrm{x}=\frac{\pi}{\mathrm{2}}+\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(−\frac{\mathrm{1}}{\mathrm{tant}}+\mathrm{tant}\right)\:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{tant}−\frac{\mathrm{1}}{\mathrm{tant}}\right)\mathrm{dt}\:\Rightarrow\mathrm{I}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{tanx}−\frac{\mathrm{1}}{\mathrm{tanx}}\right)\mathrm{dx} \\ $$$$=_{\mathrm{tanx}\:=\mathrm{u}} \:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\right)\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\right)}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\:\mathrm{du}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\right)}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du}\:=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{i}\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\right)} }{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du}\right) \\ $$$$\left.\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{i}\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}}\right)} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi−\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right) \\ $$$$=\mathrm{2i}\pi×\frac{\mathrm{e}^{\mathrm{i}\left(\mathrm{i}−\frac{\mathrm{1}}{\mathrm{i}}\right)} }{\mathrm{2i}}\:=\pi\:\mathrm{e}^{−\mathrm{1}−\mathrm{1}\:} =\pi\:\mathrm{e}^{−\mathrm{2}} \:\Rightarrow\:\bigstar\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}\left(\mathrm{tanx}−\mathrm{cotanx}\right)\mathrm{dx}=\frac{\pi}{\mathrm{e}^{\mathrm{2}} }\:\bigstar \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 26/Aug/20

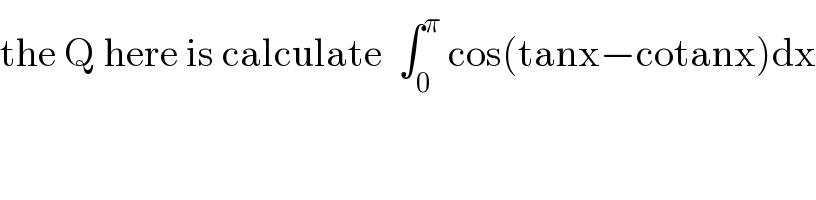
the Q here is calculate ∫_0 ^π cos(tanx−cotanx)dx

$$\mathrm{the}\:\mathrm{Q}\:\mathrm{here}\:\mathrm{is}\:\mathrm{calculate}\:\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}\left(\mathrm{tanx}−\mathrm{cotanx}\right)\mathrm{dx} \\ $$

Commented by mnjuly1970 last updated on 26/Aug/20

$${very}\:{excellent}… \\ $$

Commented by mathmax by abdo last updated on 26/Aug/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply