Question Number 109914 by 1549442205PVT last updated on 26/Aug/20

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{tan142}°\mathrm{30}'+\sqrt{\mathrm{6}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{is}\:\mathrm{an}\:\mathrm{integer}. \\ $$
Answered by Dwaipayan Shikari last updated on 26/Aug/20
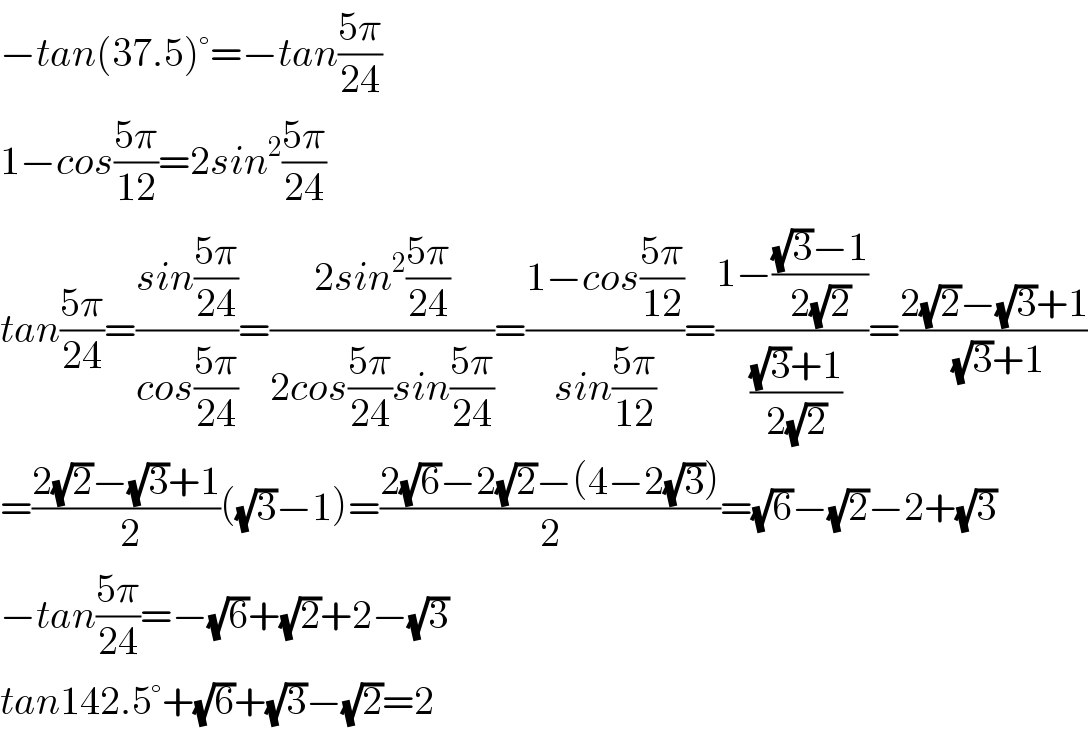
$$−{tan}\left(\mathrm{37}.\mathrm{5}\right)°=−{tan}\frac{\mathrm{5}\pi}{\mathrm{24}} \\ $$$$\mathrm{1}−{cos}\frac{\mathrm{5}\pi}{\mathrm{12}}=\mathrm{2}{sin}^{\mathrm{2}} \frac{\mathrm{5}\pi}{\mathrm{24}} \\ $$$${tan}\frac{\mathrm{5}\pi}{\mathrm{24}}=\frac{{sin}\frac{\mathrm{5}\pi}{\mathrm{24}}}{{cos}\frac{\mathrm{5}\pi}{\mathrm{24}}}=\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{\mathrm{5}\pi}{\mathrm{24}}}{\mathrm{2}{cos}\frac{\mathrm{5}\pi}{\mathrm{24}}{sin}\frac{\mathrm{5}\pi}{\mathrm{24}}}=\frac{\mathrm{1}−{cos}\frac{\mathrm{5}\pi}{\mathrm{12}}}{{sin}\frac{\mathrm{5}\pi}{\mathrm{12}}}=\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}{\:\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\mathrm{1}}{\:\mathrm{2}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)=\frac{\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{2}\sqrt{\mathrm{2}}−\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\right)}{\mathrm{2}}=\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}−\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$−{tan}\frac{\mathrm{5}\pi}{\mathrm{24}}=−\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}+\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${tan}\mathrm{142}.\mathrm{5}°+\sqrt{\mathrm{6}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}=\mathrm{2} \\ $$
Commented by 1549442205PVT last updated on 27/Aug/20

$$\mathrm{Thank}\:\mathrm{Sir}. \\ $$
