Question Number 109950 by 675480065 last updated on 26/Aug/20

Answered by Aziztisffola last updated on 26/Aug/20

$$\:\left(\mathrm{i}\right)\:\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}>\mathrm{0} \\ $$$$\:\Rightarrow\mathrm{x}^{\mathrm{2}} >\mathrm{2x}−\mathrm{1}\:\underset{\mathrm{2x}−\mathrm{1}>\mathrm{1}} {\overset{\mathrm{x}>\mathrm{1}} {\Rightarrow}}\:\:\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2x}−\mathrm{1}}>\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{g}\left(\mathrm{x}\right)>\mathrm{1} \\ $$$$\:\left(\mathrm{ii}\right)\:\mathrm{w}_{\mathrm{n}+\mathrm{1}} =\mathrm{ln}\left(\mathrm{v}_{\mathrm{n}+\mathrm{1}} \right)=\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }\right) \\ $$$$\:=\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{2u}_{\mathrm{n}} −\mathrm{1}}{\mathrm{u}_{\mathrm{n}} ^{\mathrm{2}} \:}\right)=\mathrm{ln}\left(\frac{\mathrm{u}_{\mathrm{n}} ^{\mathrm{2}} −\mathrm{2u}_{\mathrm{n}} +\mathrm{1}}{\mathrm{u}_{\mathrm{n}} ^{\mathrm{2}} }\right) \\ $$$$\:=\mathrm{ln}\left(\frac{\left(\mathrm{u}_{\mathrm{n}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{u}_{\mathrm{n}} ^{\mathrm{2}} }\right)=\mathrm{ln}\left(\left(\frac{\mathrm{u}_{\mathrm{n}} −\mathrm{1}}{\mathrm{u}_{\mathrm{n}} }\right)^{\mathrm{2}} \right) \\ $$$$\:=\mathrm{2ln}\left(\frac{\mathrm{u}_{\mathrm{n}} −\mathrm{1}}{\mathrm{u}_{\mathrm{n}} }\right)=\mathrm{2ln}\left(\mathrm{v}_{\mathrm{n}} \right)=\mathrm{2w}_{\mathrm{n}} \\ $$$$\Rightarrow\:\forall\mathrm{n}\in\mathbb{N}\:\::\:\mathrm{w}_{\mathrm{n}+\mathrm{1}} =\mathrm{2w}_{\mathrm{n}} \\ $$$$\Rightarrow\:\left(\mathrm{w}_{\mathrm{n}} \right)\:\mathrm{is}\:\mathrm{geometric}\:\mathrm{sequence}\:\mathrm{with} \\ $$$$\:\mathrm{ratio}\:\mathrm{q}=\mathrm{2}\:\mathrm{and}\:\mathrm{first}\:\mathrm{term}\:\mathrm{w}_{\mathrm{0}} =\mathrm{ln}\left(\mathrm{v}_{\mathrm{0}} \right) \\ $$$$\:\mathrm{w}_{\mathrm{0}} =\mathrm{ln}\left(\frac{\mathrm{u}_{\mathrm{0}} −\mathrm{1}}{\mathrm{u}_{\mathrm{0}} }\right)=\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{ln2}\: \\ $$
Answered by Aziztisffola last updated on 26/Aug/20
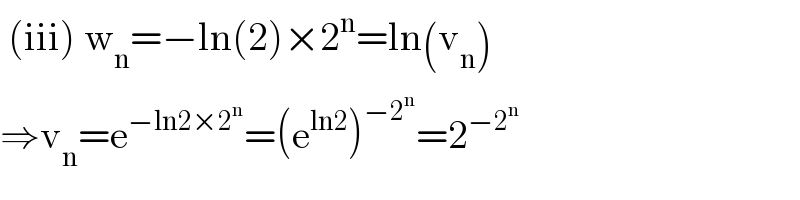
$$\:\left(\mathrm{iii}\right)\:\mathrm{w}_{\mathrm{n}} =−\mathrm{ln}\left(\mathrm{2}\right)×\mathrm{2}^{\mathrm{n}} =\mathrm{ln}\left(\mathrm{v}_{\mathrm{n}} \right) \\ $$$$\Rightarrow\mathrm{v}_{\mathrm{n}} =\mathrm{e}^{−\mathrm{ln2}×\mathrm{2}^{\mathrm{n}} } =\left(\mathrm{e}^{\mathrm{ln2}} \right)^{−\mathrm{2}^{\mathrm{n}} } =\mathrm{2}^{−\mathrm{2}^{\mathrm{n}} } \\ $$
