Question Number 175614 by leodera last updated on 03/Sep/22
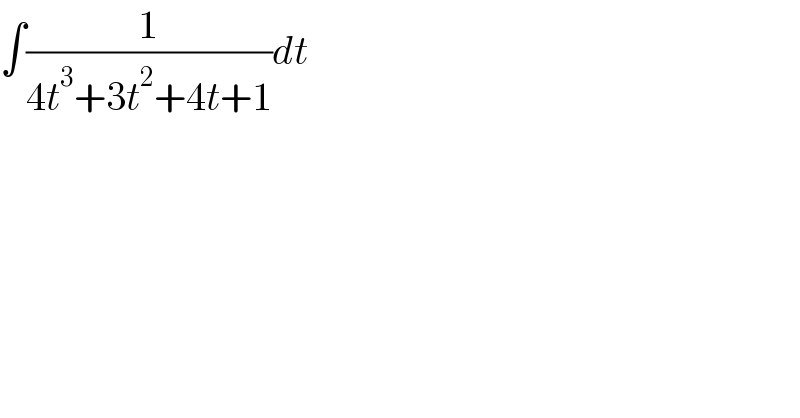
$$\int\frac{\mathrm{1}}{\mathrm{4}{t}^{\mathrm{3}} +\mathrm{3}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}}{dt} \\ $$
Answered by ajfour last updated on 04/Sep/22

$${I}=\int\frac{{dt}}{\mathrm{4}\left({t}+{p}\right)\left({t}^{\mathrm{2}} +{qt}+{r}\right)} \\ $$$$\mathrm{4}{I}=\int\frac{{Adt}}{{t}+{p}}+\frac{\left({Bt}+{C}\right){dt}}{{t}^{\mathrm{2}} +{qt}+{r}} \\ $$$$\:\:\mathrm{4}{I}\:={A}\mathrm{ln}\:\left({t}+{p}\right)+\frac{{B}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +{qt}+{r}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{s}\mathrm{tan}^{−\mathrm{1}} \frac{{t}+\frac{{q}}{\mathrm{2}}}{\:\sqrt{{r}−\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}}+{c} \\ $$$${differentiating} \\ $$$$\frac{{A}}{{t}+{p}}+\frac{{B}\left({t}+\frac{{q}}{\mathrm{2}}\right)}{{t}^{\mathrm{2}} +{qt}+{r}}+\frac{{s}\sqrt{{r}−\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}}{\left({t}+\frac{{q}}{\mathrm{2}}\right)^{\mathrm{2}} +{r}−\frac{{q}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\frac{{A}\left({t}^{\mathrm{2}} +{qt}+{r}\right)+{B}\left({t}+\frac{{q}}{\mathrm{2}}\right)\left({t}+{p}\right)+{s}\sqrt{{r}−\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}}{\left({t}+{p}\right)\left({t}^{\mathrm{2}} +{qt}+{r}\right)} \\ $$$$=\frac{\mathrm{1}}{{t}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{4}}{t}^{\mathrm{2}} +{t}+\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${compare}\:{to}\:{find} \\ $$$${p},\:{q},\:{r},\:{A},\:{B},\:{s} \\ $$$$ \\ $$
