Question Number 44575 by Raj Singh last updated on 01/Oct/18

Commented by $@ty@m last updated on 01/Oct/18

$${similar}\:{to}\:{Q}.\:{No}.\:\mathrm{41703} \\ $$
Commented by Raj Singh last updated on 02/Oct/18

$${this}\:{is}\:{sin}\mathrm{2}\Theta \\ $$
Commented by $@ty@m last updated on 02/Oct/18

$${it}\:{doesn}'{t}\:{matter}. \\ $$$$\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2sin}\:\theta\mathrm{cos}\:\theta \\ $$$${when}\:{divided}\:{by}\:\mathrm{cos}\:^{\mathrm{4}} \theta, \\ $$$${N}^{{r}} =\mathrm{2tan}\:\theta.\mathrm{sec}\:^{\mathrm{2}} \theta \\ $$$$….\:{and}\:{then}\:{the}\:{procedure}\:{will}\: \\ $$$${be}\:{similar}. \\ $$$$….\:{our}\:{ultimate}\:{aim}\:{is}\:{to}\:{get}\:\mathrm{tan}\:\theta\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Oct/18
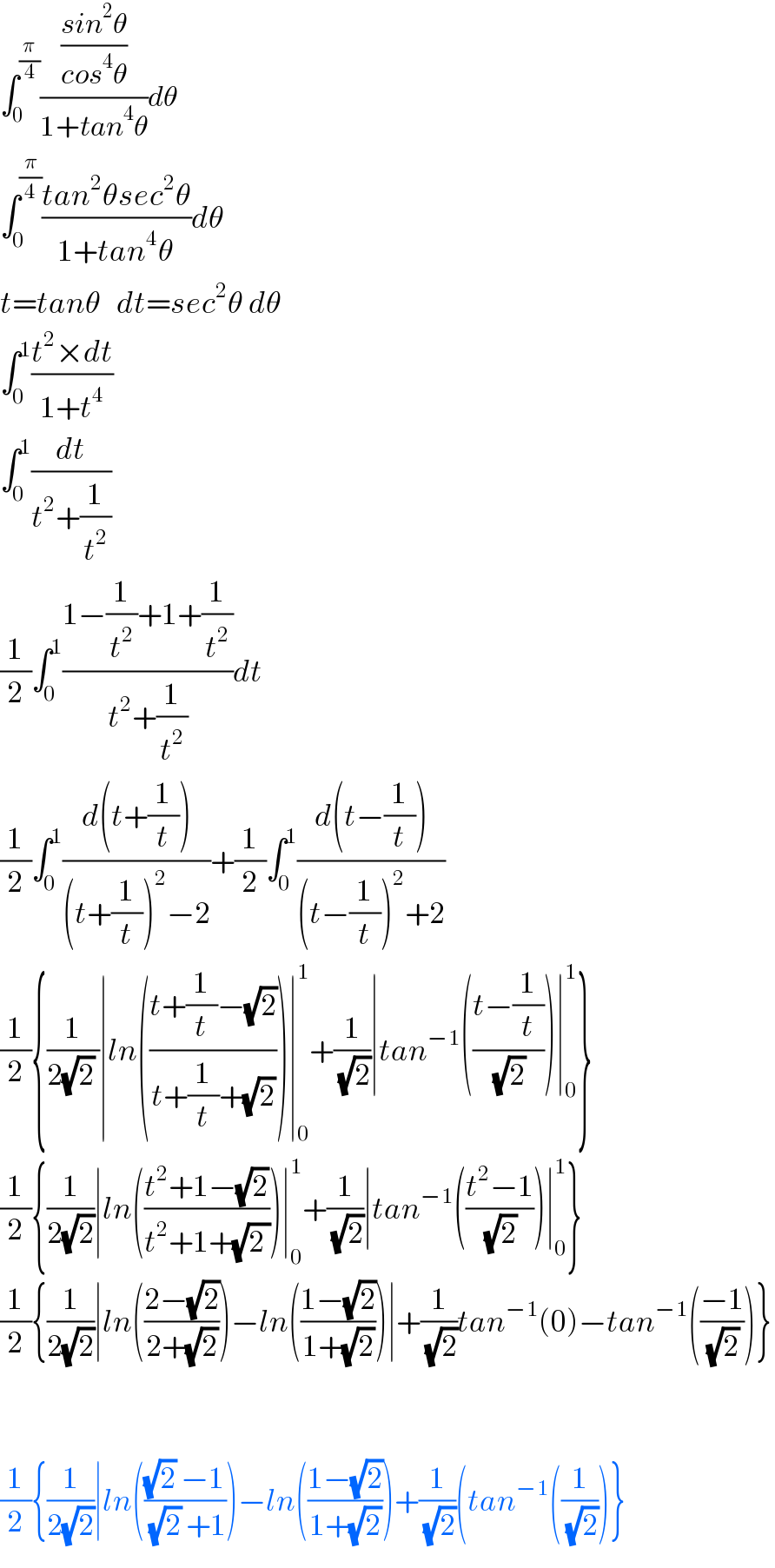
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\frac{{sin}^{\mathrm{2}} \theta}{{cos}^{\mathrm{4}} \theta}}{\mathrm{1}+{tan}^{\mathrm{4}} \theta}{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{tan}^{\mathrm{2}} \theta{sec}^{\mathrm{2}} \theta}{\mathrm{1}+{tan}^{\mathrm{4}} \theta}{d}\theta \\ $$$${t}={tan}\theta\:\:\:{dt}={sec}^{\mathrm{2}} \theta\:{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} ×{dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}\left({t}+\frac{\mathrm{1}}{{t}}\right)}{\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}\left({t}−\frac{\mathrm{1}}{{t}}\right)}{\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\:}\mid{ln}\left(\frac{{t}+\frac{\mathrm{1}}{{t}}−\sqrt{\mathrm{2}}}{{t}+\frac{\mathrm{1}}{{t}}+\sqrt{\mathrm{2}}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{t}−\frac{\mathrm{1}}{{t}}}{\:\sqrt{\mathrm{2}}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mid{ln}\left(\frac{{t}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{2}\:}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mid{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)−{ln}\left(\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)\mid+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\mathrm{0}\right)−{tan}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right\} \\ $$$$ \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mid{ln}\left(\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\:\sqrt{\mathrm{2}}\:+\mathrm{1}}\right)−{ln}\left(\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left({tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right\}\right. \\ $$
