Menu Close

Question-44795

Tinku Tara 0 Comments
Pin




Question Number 44795 by behi83417@gmail.com last updated on 04/Oct/18
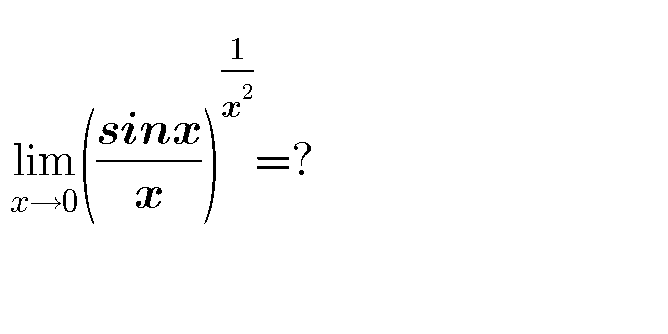
Commented by maxmathsup by imad last updated on 05/Oct/18
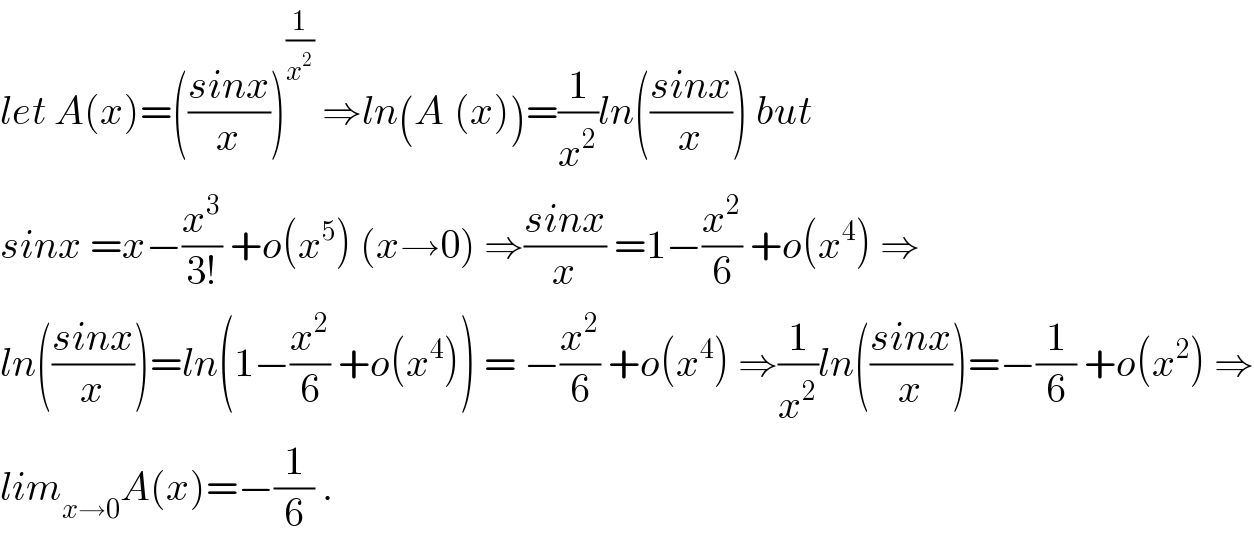
let A(x)=(((sinx)/x))^(1/x^2 ) ⇒ln(A_ (x))=(1/x^2 )ln(((sinx)/x)) but sinx =x−(x^3 /(3!)) +o(x^5 ) (x→0) ⇒((sinx)/x) =1−(x^2 /6) +o(x^4 ) ⇒ ln(((sinx)/x))=ln(1−(x^2 /6) +o(x^4 )) = −(x^2 /6) +o(x^4 ) ⇒(1/x^2 )ln(((sinx)/x))=−(1/6) +o(x^2 ) ⇒ lim_(x→0) A(x)=−(1/6) .
$${let}\:{A}\left({x}\right)=\left(\frac{{sinx}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:\Rightarrow{ln}\left({A}_{} \left({x}\right)\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left(\frac{{sinx}}{{x}}\right)\:{but} \\ $$$${sinx}\:={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+{o}\left({x}^{\mathrm{5}} \right)\:\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow\frac{{sinx}}{{x}}\:=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow \\ $$$${ln}\left(\frac{{sinx}}{{x}}\right)={ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{4}} \right)\right)\:=\:−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left(\frac{{sinx}}{{x}}\right)=−\frac{\mathrm{1}}{\mathrm{6}}\:+{o}\left({x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {A}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{6}}\:. \\ $$
Commented by maxmathsup by imad last updated on 05/Oct/18
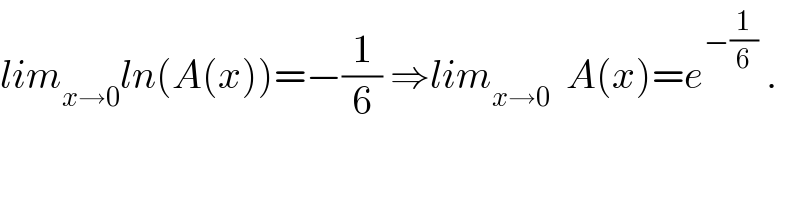
lim_(x→0) ln(A(x))=−(1/6) ⇒lim_(x→0) A(x)=e^(−(1/6)) .
$${lim}_{{x}\rightarrow\mathrm{0}} {ln}\left({A}\left({x}\right)\right)=−\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{A}\left({x}\right)={e}^{−\frac{\mathrm{1}}{\mathrm{6}}} \:. \\ $$
Commented by behi83417@gmail.com last updated on 05/Oct/18
thank you so much dear prop.abdo.
$${thank}\:{you}\:{so}\:{much}\:{dear}\:{prop}.{abdo}. \\ $$
Commented by maxmathsup by imad last updated on 05/Oct/18
you are welcome sir behi.
$${you}\:{are}\:{welcome}\:{sir}\:{behi}. \\ $$
Answered by ajfour last updated on 04/Oct/18
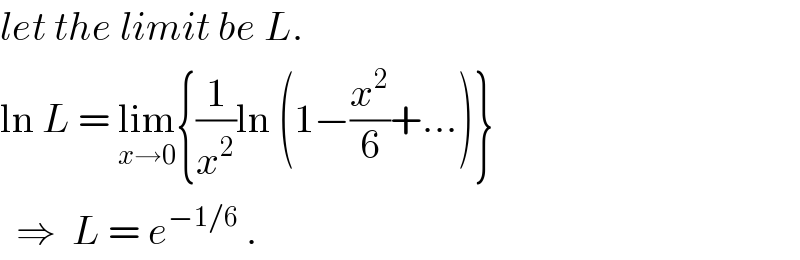
let the limit be L. ln L = lim_(x→0) {(1/x^2 )ln (1−(x^2 /6)+...)} ⇒ L = e^(−1/6) .
$${let}\:{the}\:{limit}\:{be}\:{L}. \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\mathrm{ln}\:\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+…\right)\right\} \\ $$$$\:\:\Rightarrow\:\:{L}\:=\:{e}^{−\mathrm{1}/\mathrm{6}} \:. \\ $$
Commented by behi83417@gmail.com last updated on 04/Oct/18
thank you very much sir Ajfour.
$${thank}\:{you}\:{very}\:{much}\:{sir}\:{Ajfour}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *