A-tangent-to-ellipse-x-2-a-2-y-2-b-2-1-at-point-p-meets-the-minor-axis-at-L-if-the-normal-at-p-meets-the-major-axis-at-m-find-the-locus-of-midpoint-LM-

Question Number 44988 by peter frank last updated on 07/Oct/18

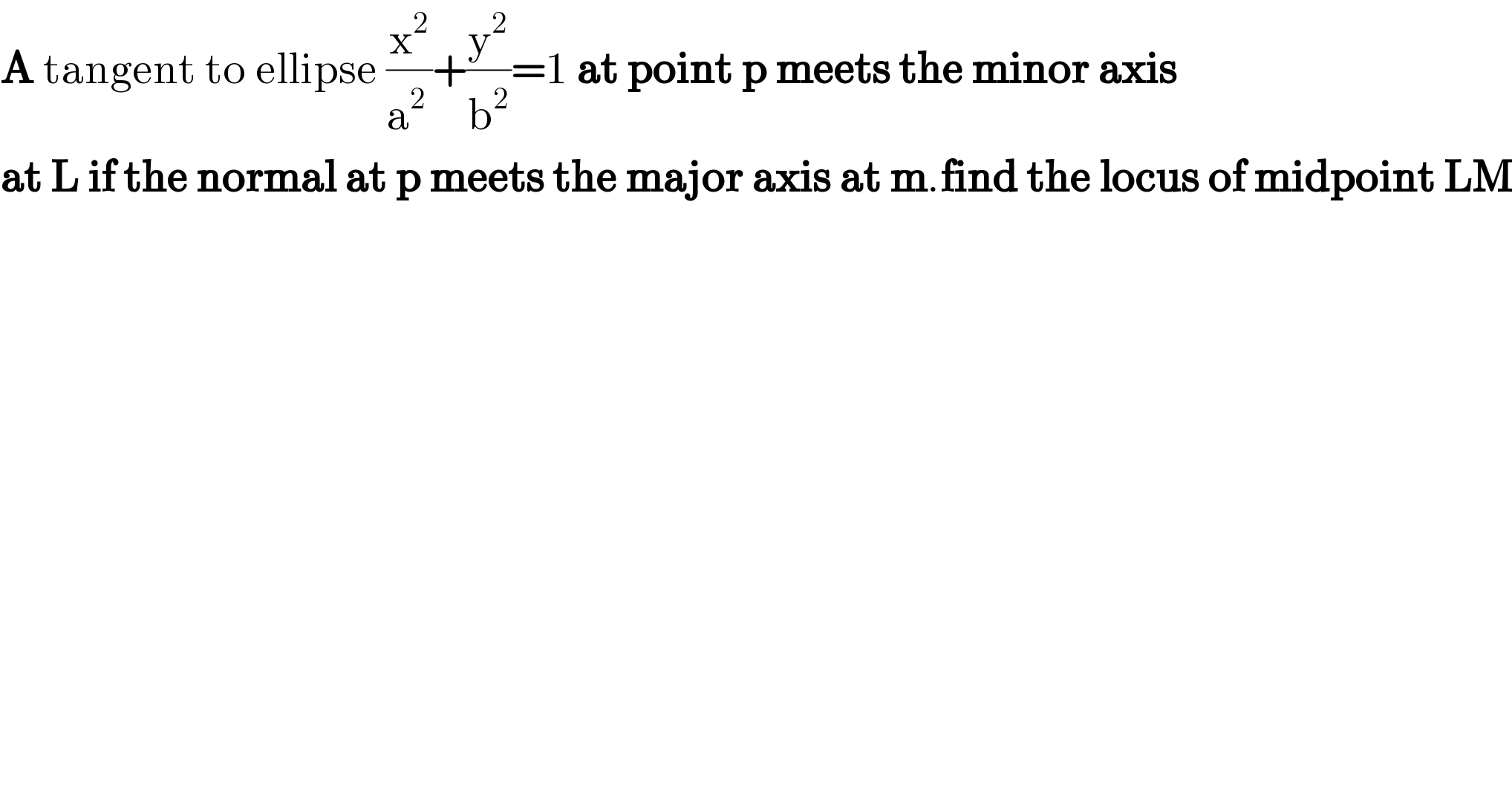
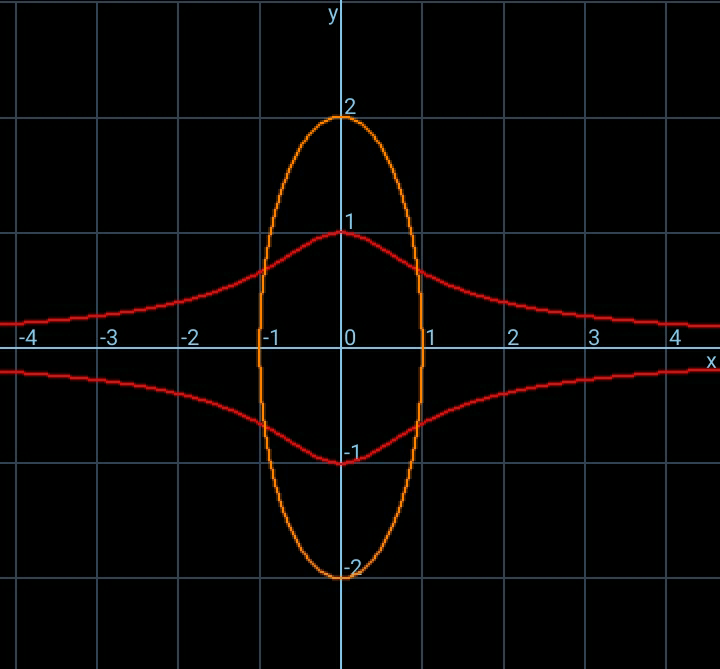
$$\boldsymbol{\mathrm{A}}\:\mathrm{tangent}\:\mathrm{to}\:\mathrm{ellipse}\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}\:} }+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }=\mathrm{1}\:\boldsymbol{\mathrm{at}}\:\boldsymbol{\mathrm{point}}\:\boldsymbol{\mathrm{p}}\:\boldsymbol{\mathrm{meets}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{minor}}\:\boldsymbol{\mathrm{axis}} \\ $$$$\boldsymbol{\mathrm{at}}\:\boldsymbol{\mathrm{L}}\:\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{normal}}\:\boldsymbol{\mathrm{at}}\:\boldsymbol{\mathrm{p}}\:\boldsymbol{\mathrm{meets}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{major}}\:\boldsymbol{\mathrm{axis}}\:\boldsymbol{\mathrm{at}}\:\boldsymbol{\mathrm{m}}.\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{locus}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{midpoint}}\:\boldsymbol{\mathrm{LM}} \\ $$

Answered by MrW3 last updated on 07/Oct/18

(x^2 /a^2 )+(y^2 /b^2 )=1 ((2x)/a^2 )+((2y)/b^2 )×(dy/dx)=1 (dy/dx)=−((b^2 x)/(a^2 y)) Point P(u,v) (u^2 /a^2 )+(v^2 /b^2 )=1 ...(i) eqn. of tangent PL: ((y−v)/(x−u))=−((b^2 u)/(a^2 v)) Point L(0,y_1 ) ((y_1 −v)/(−u))=−((b^2 u)/(a^2 v)) ⇒y_1 =v(1+((b^2 u^2 )/(a^2 v^2 ))) eqn. of normal PM: ((y−v)/(x−u))=((a^2 v)/(b^2 u)) Point M(x_2 ,0) ((−v)/(x_2 −u))=((a^2 v)/(b^2 u)) ⇒x_2 =u(1−(b^2 /a^2 )) Midpoint of LM is (p,q) with p=(x_2 /2)=(u/2)(1−(b^2 /a^2 ))=((u(a^2 −b^2 ))/(2a^2 )) q=(y_1 /2)=(v/2)(1+((b^2 u^2 )/(a^2 v^2 )))=(v/2)((v^2 /b^2 )+(u^2 /a^2 ))(b^2 /v^2 )=(b^2 /(2v)) ⇒u=((2a^2 p)/(a^2 −b^2 )) ⇒v=(b^2 /(2q)) putting this into (i): ((4a^4 p^2 )/((a^2 −b^2 )a^2 ))+(b^4 /(4q^2 b^2 ))=1 ⇒((4a^2 p^2 )/(a^2 −b^2 ))+(b^2 /(4q^2 ))=1 or ⇒((4a^2 x^2 )/(a^2 −b^2 ))+(b^2 /(4y^2 ))=1

$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{2}{x}}{{a}^{\mathrm{2}} }+\frac{\mathrm{2}{y}}{{b}^{\mathrm{2}} }×\frac{{dy}}{{dx}}=\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}=−\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} {y}} \\ $$$${Point}\:{P}\left({u},{v}\right) \\ $$$$\frac{{u}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{v}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:\:\:…\left({i}\right) \\ $$$${eqn}.\:{of}\:{tangent}\:{PL}: \\ $$$$\frac{{y}−{v}}{{x}−{u}}=−\frac{{b}^{\mathrm{2}} {u}}{{a}^{\mathrm{2}} {v}} \\ $$$${Point}\:{L}\left(\mathrm{0},{y}_{\mathrm{1}} \right) \\ $$$$\frac{{y}_{\mathrm{1}} −{v}}{−{u}}=−\frac{{b}^{\mathrm{2}} {u}}{{a}^{\mathrm{2}} {v}} \\ $$$$\Rightarrow{y}_{\mathrm{1}} ={v}\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} {u}^{\mathrm{2}} }{{a}^{\mathrm{2}} {v}^{\mathrm{2}} }\right) \\ $$$${eqn}.\:{of}\:{normal}\:{PM}: \\ $$$$\frac{{y}−{v}}{{x}−{u}}=\frac{{a}^{\mathrm{2}} {v}}{{b}^{\mathrm{2}} {u}} \\ $$$${Point}\:{M}\left({x}_{\mathrm{2}} ,\mathrm{0}\right) \\ $$$$\frac{−{v}}{{x}_{\mathrm{2}} −{u}}=\frac{{a}^{\mathrm{2}} {v}}{{b}^{\mathrm{2}} {u}} \\ $$$$\Rightarrow{x}_{\mathrm{2}} ={u}\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$${Midpoint}\:{of}\:{LM}\:{is}\:\left({p},{q}\right)\:{with} \\ $$$${p}=\frac{{x}_{\mathrm{2}} }{\mathrm{2}}=\frac{{u}}{\mathrm{2}}\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)=\frac{{u}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\mathrm{2}{a}^{\mathrm{2}} } \\ $$$${q}=\frac{{y}_{\mathrm{1}} }{\mathrm{2}}=\frac{{v}}{\mathrm{2}}\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} {u}^{\mathrm{2}} }{{a}^{\mathrm{2}} {v}^{\mathrm{2}} }\right)=\frac{{v}}{\mathrm{2}}\left(\frac{{v}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\frac{{u}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\frac{{b}^{\mathrm{2}} }{{v}^{\mathrm{2}} }=\frac{{b}^{\mathrm{2}} }{\mathrm{2}{v}} \\ $$$$\Rightarrow{u}=\frac{\mathrm{2}{a}^{\mathrm{2}} {p}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{v}=\frac{{b}^{\mathrm{2}} }{\mathrm{2}{q}} \\ $$$${putting}\:{this}\:{into}\:\left({i}\right): \\ $$$$\frac{\mathrm{4}{a}^{\mathrm{4}} {p}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){a}^{\mathrm{2}} }+\frac{{b}^{\mathrm{4}} }{\mathrm{4}{q}^{\mathrm{2}} {b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{4}{a}^{\mathrm{2}} {p}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }+\frac{{b}^{\mathrm{2}} }{\mathrm{4}{q}^{\mathrm{2}} }=\mathrm{1} \\ $$$${or} \\ $$$$\Rightarrow\frac{\mathrm{4}{a}^{\mathrm{2}} {x}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }+\frac{{b}^{\mathrm{2}} }{\mathrm{4}{y}^{\mathrm{2}} }=\mathrm{1} \\ $$

Commented by peter frank last updated on 07/Oct/18

thank you once gain sir.i really appreciate your effort

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{once}\:\mathrm{gain}\:\mathrm{sir}.\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort} \\ $$

Commented by MrW3 last updated on 07/Oct/18