Question Number 110551 by shahria14 last updated on 29/Aug/20
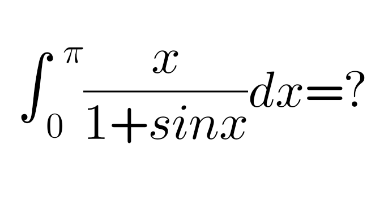
Answered by Dwaipayan Shikari last updated on 29/Aug/20
![∫_0 ^π (x/(1+sinx))dx=∫_0 ^π ((π−x)/(1+sinx))dx=I 2I=∫_0 ^π (π/(1+sinx))dx=2π∫_0 ^∞ (1/(1+((2t)/(1+t^2 )))).(1/(1+t^2 ))dt (tan(x/2)=t) 2I=2π∫_0 ^∞ (1/((1+t)^2 ))dt I=−π[(1/(1+t))]_0 ^∞ =π](https://www.tinkutara.com/question/Q110554.png)
$$\int_{\mathrm{0}} ^{\pi} \frac{{x}}{\mathrm{1}+{sinx}}{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\pi−{x}}{\mathrm{1}+{sinx}}{dx}={I} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{1}+{sinx}}{dx}=\mathrm{2}\pi\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:\:\:\:\:\:\left({tan}\frac{{x}}{\mathrm{2}}={t}\right) \\ $$$$\mathrm{2}{I}=\mathrm{2}\pi\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$${I}=−\pi\left[\frac{\mathrm{1}}{\mathrm{1}+{t}}\right]_{\mathrm{0}} ^{\infty} =\pi \\ $$
Answered by mathmax by abdo last updated on 30/Aug/20
![I =∫_0 ^π ((xdx)/(1+sinx)) changement x =π−t give I =∫_0 ^π ((π−t)/(1+sint)) dt =π ∫_0 ^(π ) (dt/(1+sint)) −I ⇒2I =π∫_0 ^π (dt/(1+sint)) =_(tan((t/2))=u) ∫_0 ^∞ ((2du)/((1+u^2 )(1+((2u)/(1+u^2 ))))) =∫_0 ^∞ ((2du)/(1+u^2 +2u)) =2∫_0 ^∞ (du/((1+u)^2 )) =[((−2)/(1+u))]_0 ^∞ =1 ⇒2I =π ⇒I =(π/2)](https://www.tinkutara.com/question/Q110685.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{xdx}}{\mathrm{1}+\mathrm{sinx}}\:\mathrm{changement}\:\mathrm{x}\:=\pi−\mathrm{t}\:\mathrm{give}\: \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{\pi−\mathrm{t}}{\mathrm{1}+\mathrm{sint}}\:\mathrm{dt}\:=\pi\:\int_{\mathrm{0}} ^{\pi\:} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{sint}}\:−\mathrm{I}\:\Rightarrow\mathrm{2I}\:=\pi\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{sint}} \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}} \:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} \:+\mathrm{2u}}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} } \\ $$$$=\left[\frac{−\mathrm{2}}{\mathrm{1}+\mathrm{u}}\right]_{\mathrm{0}} ^{\infty} \:=\mathrm{1}\:\Rightarrow\mathrm{2I}\:=\pi\:\Rightarrow\mathrm{I}\:=\frac{\pi}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 30/Aug/20

$$\mathrm{sorry}\:\mathrm{2I}\:=\mathrm{2}\pi\:\Rightarrow\:\mathrm{I}\:=\pi \\ $$
