Menu Close

Two-polynomials-P-and-Q-satisfy-P-2x-Q-x-Q-2x-P-x-Given-that-Q-x-x-2-4-and-P-x-ax-b-Find-2a-b-

Tinku Tara 0 Comments
Pin




Question Number 110675 by Aina Samuel Temidayo last updated on 30/Aug/20
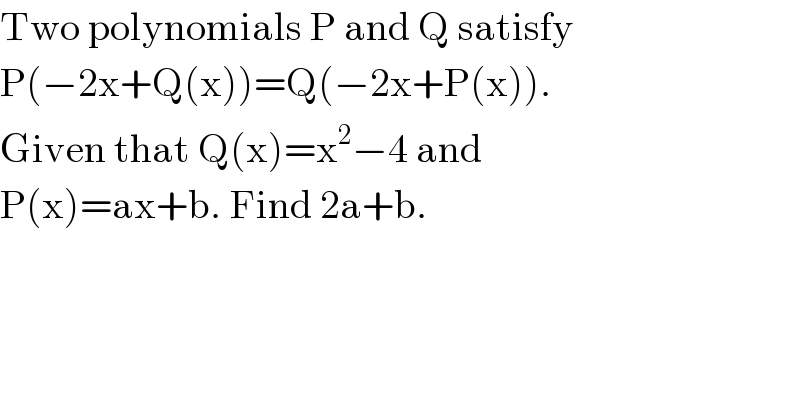
Two polynomials P and Q satisfy P(−2x+Q(x))=Q(−2x+P(x)). Given that Q(x)=x^2 −4 and P(x)=ax+b. Find 2a+b.
$$\mathrm{Two}\:\mathrm{polynomials}\:\mathrm{P}\:\mathrm{and}\:\mathrm{Q}\:\mathrm{satisfy} \\ $$$$\mathrm{P}\left(−\mathrm{2x}+\mathrm{Q}\left(\mathrm{x}\right)\right)=\mathrm{Q}\left(−\mathrm{2x}+\mathrm{P}\left(\mathrm{x}\right)\right). \\ $$$$\mathrm{Given}\:\mathrm{that}\:\mathrm{Q}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{4}\:\mathrm{and} \\ $$$$\mathrm{P}\left(\mathrm{x}\right)=\mathrm{ax}+\mathrm{b}.\:\mathrm{Find}\:\mathrm{2a}+\mathrm{b}. \\ $$
Answered by bemath last updated on 30/Aug/20
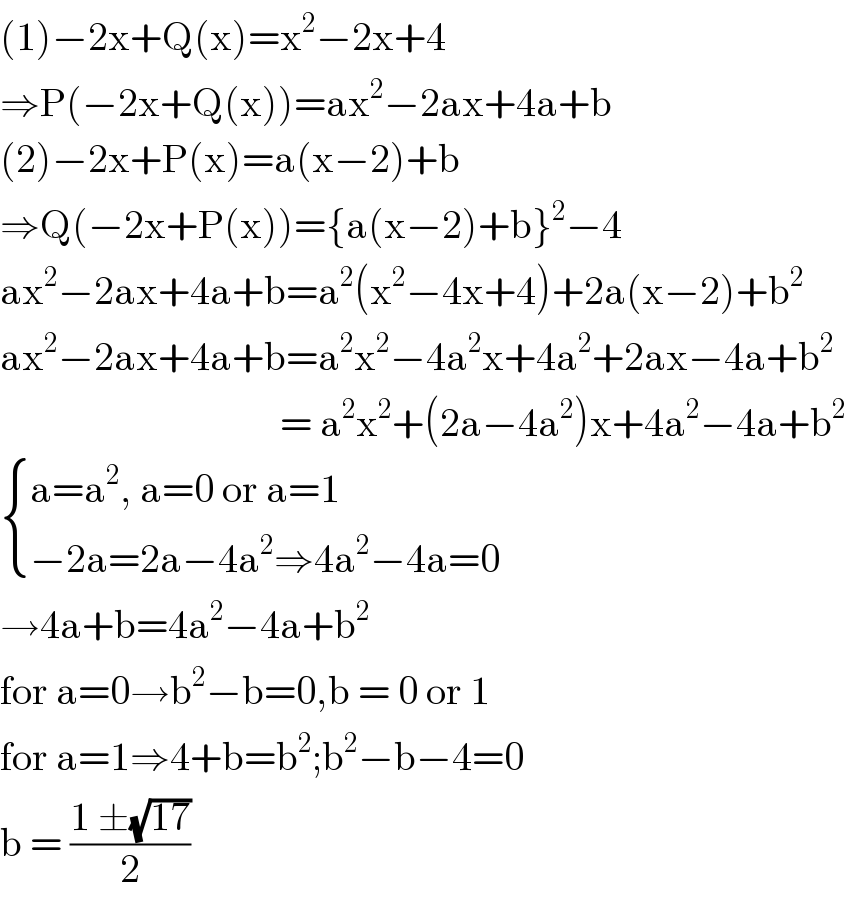
(1)−2x+Q(x)=x^2 −2x+4 ⇒P(−2x+Q(x))=ax^2 −2ax+4a+b (2)−2x+P(x)=a(x−2)+b ⇒Q(−2x+P(x))={a(x−2)+b}^2 −4 ax^2 −2ax+4a+b=a^2 (x^2 −4x+4)+2a(x−2)+b^2 ax^2 −2ax+4a+b=a^2 x^2 −4a^2 x+4a^2 +2ax−4a+b^2 = a^2 x^2 +(2a−4a^2 )x+4a^2 −4a+b^2 { ((a=a^2 , a=0 or a=1)),((−2a=2a−4a^2 ⇒4a^2 −4a=0)) :} →4a+b=4a^2 −4a+b^2 for a=0→b^2 −b=0,b = 0 or 1 for a=1⇒4+b=b^2 ;b^2 −b−4=0 b = ((1 ±(√(17)))/2)
$$\left(\mathrm{1}\right)−\mathrm{2x}+\mathrm{Q}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{4} \\ $$$$\Rightarrow\mathrm{P}\left(−\mathrm{2x}+\mathrm{Q}\left(\mathrm{x}\right)\right)=\mathrm{ax}^{\mathrm{2}} −\mathrm{2ax}+\mathrm{4a}+\mathrm{b} \\ $$$$\left(\mathrm{2}\right)−\mathrm{2x}+\mathrm{P}\left(\mathrm{x}\right)=\mathrm{a}\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{b} \\ $$$$\Rightarrow\mathrm{Q}\left(−\mathrm{2x}+\mathrm{P}\left(\mathrm{x}\right)\right)=\left\{\mathrm{a}\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{b}\right\}^{\mathrm{2}} −\mathrm{4} \\ $$$$\mathrm{ax}^{\mathrm{2}} −\mathrm{2ax}+\mathrm{4a}+\mathrm{b}=\mathrm{a}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}\right)+\mathrm{2a}\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{b}^{\mathrm{2}} \\ $$$$\mathrm{ax}^{\mathrm{2}} −\mathrm{2ax}+\mathrm{4a}+\mathrm{b}=\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{4a}^{\mathrm{2}} \mathrm{x}+\mathrm{4a}^{\mathrm{2}} +\mathrm{2ax}−\mathrm{4a}+\mathrm{b}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +\left(\mathrm{2a}−\mathrm{4a}^{\mathrm{2}} \right)\mathrm{x}+\mathrm{4a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{b}^{\mathrm{2}} \\ $$$$\begin{cases}{\mathrm{a}=\mathrm{a}^{\mathrm{2}} ,\:\mathrm{a}=\mathrm{0}\:\mathrm{or}\:\mathrm{a}=\mathrm{1}}\\{−\mathrm{2a}=\mathrm{2a}−\mathrm{4a}^{\mathrm{2}} \Rightarrow\mathrm{4a}^{\mathrm{2}} −\mathrm{4a}=\mathrm{0}}\end{cases} \\ $$$$\rightarrow\mathrm{4a}+\mathrm{b}=\mathrm{4a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{b}^{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{a}=\mathrm{0}\rightarrow\mathrm{b}^{\mathrm{2}} −\mathrm{b}=\mathrm{0},\mathrm{b}\:=\:\mathrm{0}\:\mathrm{or}\:\mathrm{1} \\ $$$$\mathrm{for}\:\mathrm{a}=\mathrm{1}\Rightarrow\mathrm{4}+\mathrm{b}=\mathrm{b}^{\mathrm{2}} ;\mathrm{b}^{\mathrm{2}} −\mathrm{b}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{b}\:=\:\frac{\mathrm{1}\:\pm\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$
Commented by Aina Samuel Temidayo last updated on 30/Aug/20
Thanks but with the options I have here, the answer should be an integer.
$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{with}\:\mathrm{the}\:\mathrm{options}\:\mathrm{I}\:\mathrm{have} \\ $$$$\mathrm{here},\:\mathrm{the}\:\mathrm{answer}\:\mathrm{should}\:\mathrm{be}\:\mathrm{an}\:\mathrm{integer}. \\ $$
Commented by bemath last updated on 30/Aug/20
what reason the answer should be integer? given di condition?
$$\mathrm{what}\:\mathrm{reason}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{should}\:\mathrm{be}\:\mathrm{integer}?\:\mathrm{given}\:\mathrm{di}\:\mathrm{condition}? \\ $$
Commented by Aina Samuel Temidayo last updated on 30/Aug/20
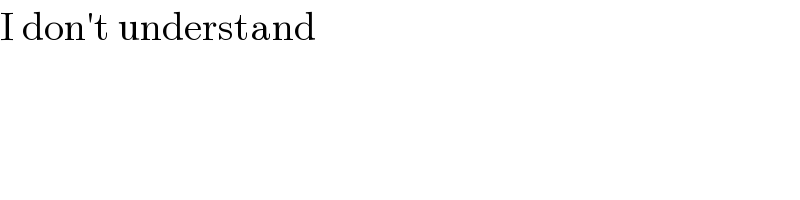
I don′t understand
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand} \\ $$
Commented by floor(10²Eta[1]) last updated on 30/Aug/20
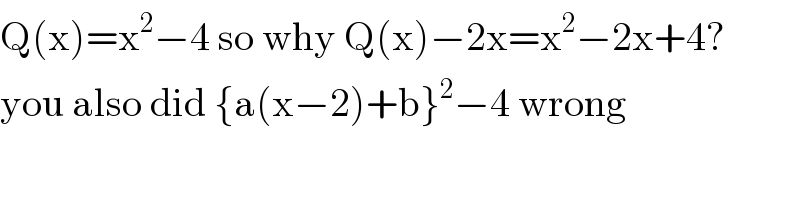
Q(x)=x^2 −4 so why Q(x)−2x=x^2 −2x+4? you also did {a(x−2)+b}^2 −4 wrong
$$\mathrm{Q}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{4}\:\mathrm{so}\:\mathrm{why}\:\mathrm{Q}\left(\mathrm{x}\right)−\mathrm{2x}=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{4}? \\ $$$$\mathrm{you}\:\mathrm{also}\:\mathrm{did}\:\left\{\mathrm{a}\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{b}\right\}^{\mathrm{2}} −\mathrm{4}\:\mathrm{wrong} \\ $$
Commented by Aina Samuel Temidayo last updated on 30/Aug/20
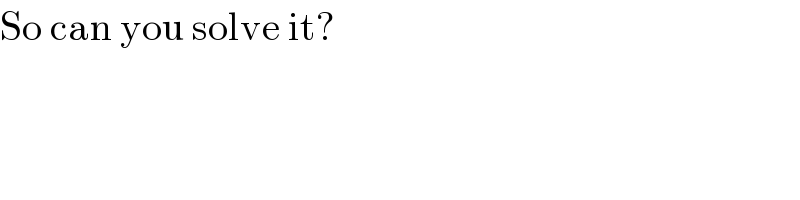
So can you solve it?
$$\mathrm{So}\:\mathrm{can}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{it}? \\ $$
Commented by bemath last updated on 30/Aug/20
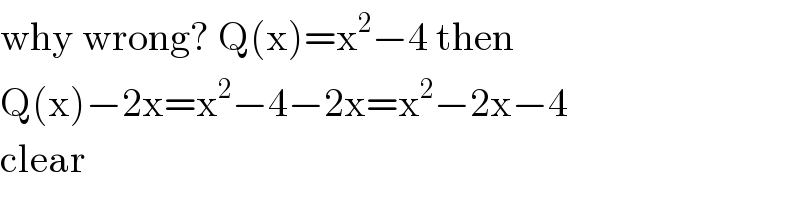
why wrong? Q(x)=x^2 −4 then Q(x)−2x=x^2 −4−2x=x^2 −2x−4 clear
$$\mathrm{why}\:\mathrm{wrong}?\:\mathrm{Q}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{4}\:\mathrm{then}\: \\ $$$$\mathrm{Q}\left(\mathrm{x}\right)−\mathrm{2x}=\mathrm{x}^{\mathrm{2}} −\mathrm{4}−\mathrm{2x}=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{4} \\ $$$$\mathrm{clear} \\ $$
Commented by floor(10²Eta[1]) last updated on 30/Aug/20
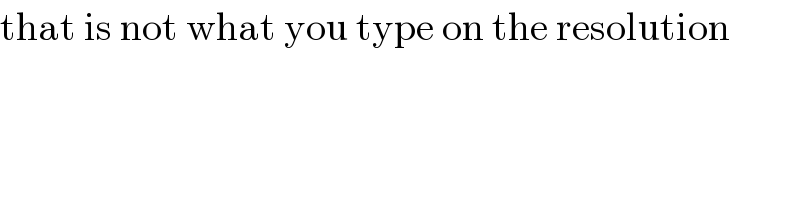
that is not what you type on the resolution
$$\mathrm{that}\:\mathrm{is}\:\mathrm{not}\:\mathrm{what}\:\mathrm{you}\:\mathrm{type}\:\mathrm{on}\:\mathrm{the}\:\mathrm{resolution} \\ $$
Answered by Aziztisffola last updated on 30/Aug/20
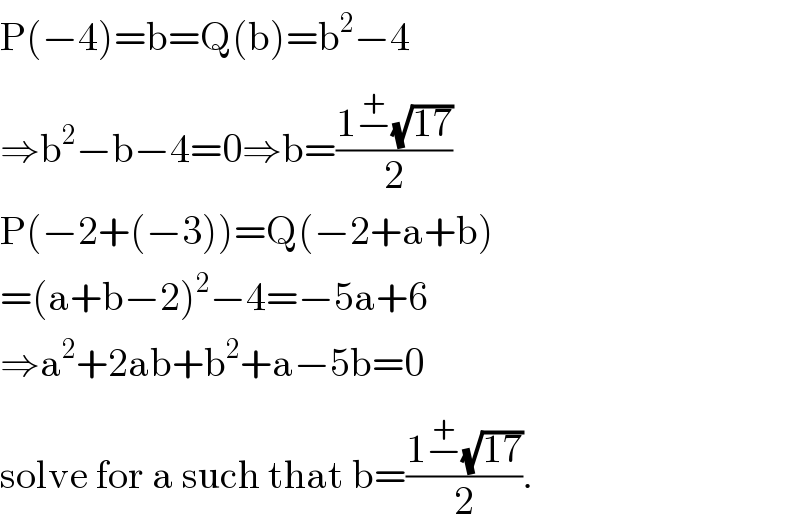
P(−4)=b=Q(b)=b^2 −4 ⇒b^2 −b−4=0⇒b=((1−^(+) (√(17)))/2) P(−2+(−3))=Q(−2+a+b) =(a+b−2)^2 −4=−5a+6 ⇒a^2 +2ab+b^2 +a−5b=0 solve for a such that b=((1−^(+) (√(17)))/2).
$$\mathrm{P}\left(−\mathrm{4}\right)=\mathrm{b}=\mathrm{Q}\left(\mathrm{b}\right)=\mathrm{b}^{\mathrm{2}} −\mathrm{4} \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} −\mathrm{b}−\mathrm{4}=\mathrm{0}\Rightarrow\mathrm{b}=\frac{\mathrm{1}\overset{+} {−}\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\mathrm{P}\left(−\mathrm{2}+\left(−\mathrm{3}\right)\right)=\mathrm{Q}\left(−\mathrm{2}+\mathrm{a}+\mathrm{b}\right) \\ $$$$=\left(\mathrm{a}+\mathrm{b}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}=−\mathrm{5a}+\mathrm{6} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{2ab}+\mathrm{b}^{\mathrm{2}} +\mathrm{a}−\mathrm{5b}=\mathrm{0} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{a}\:\mathrm{such}\:\mathrm{that}\:\mathrm{b}=\frac{\mathrm{1}\overset{+} {−}\sqrt{\mathrm{17}}}{\mathrm{2}}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *