Question-176318

Question Number 176318 by Matica last updated on 16/Sep/22

Commented by Rasheed.Sindhi last updated on 16/Sep/22

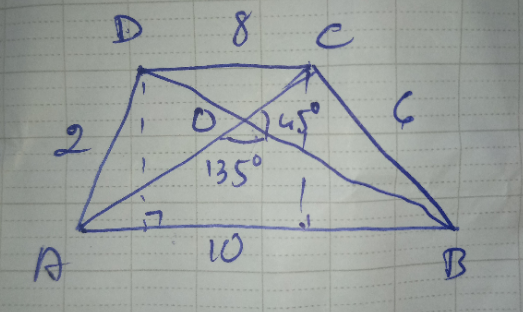
$${find}\:{area}\:{of}\:{quadrilateral}\:\mathrm{ABCD} \\ $$

Commented by mr W last updated on 16/Sep/22

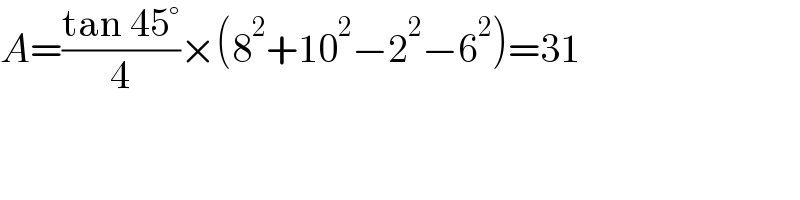
A=((tan 45°)/4)×(8^2 +10^2 −2^2 −6^2 )=31

$${A}=\frac{\mathrm{tan}\:\mathrm{45}°}{\mathrm{4}}×\left(\mathrm{8}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} −\mathrm{6}^{\mathrm{2}} \right)=\mathrm{31} \\ $$

Commented by Matica last updated on 16/Sep/22

$${please}\:{say}\:{more}\:{detail} \\ $$

Answered by mr W last updated on 16/Sep/22

Commented by mr W last updated on 16/Sep/22

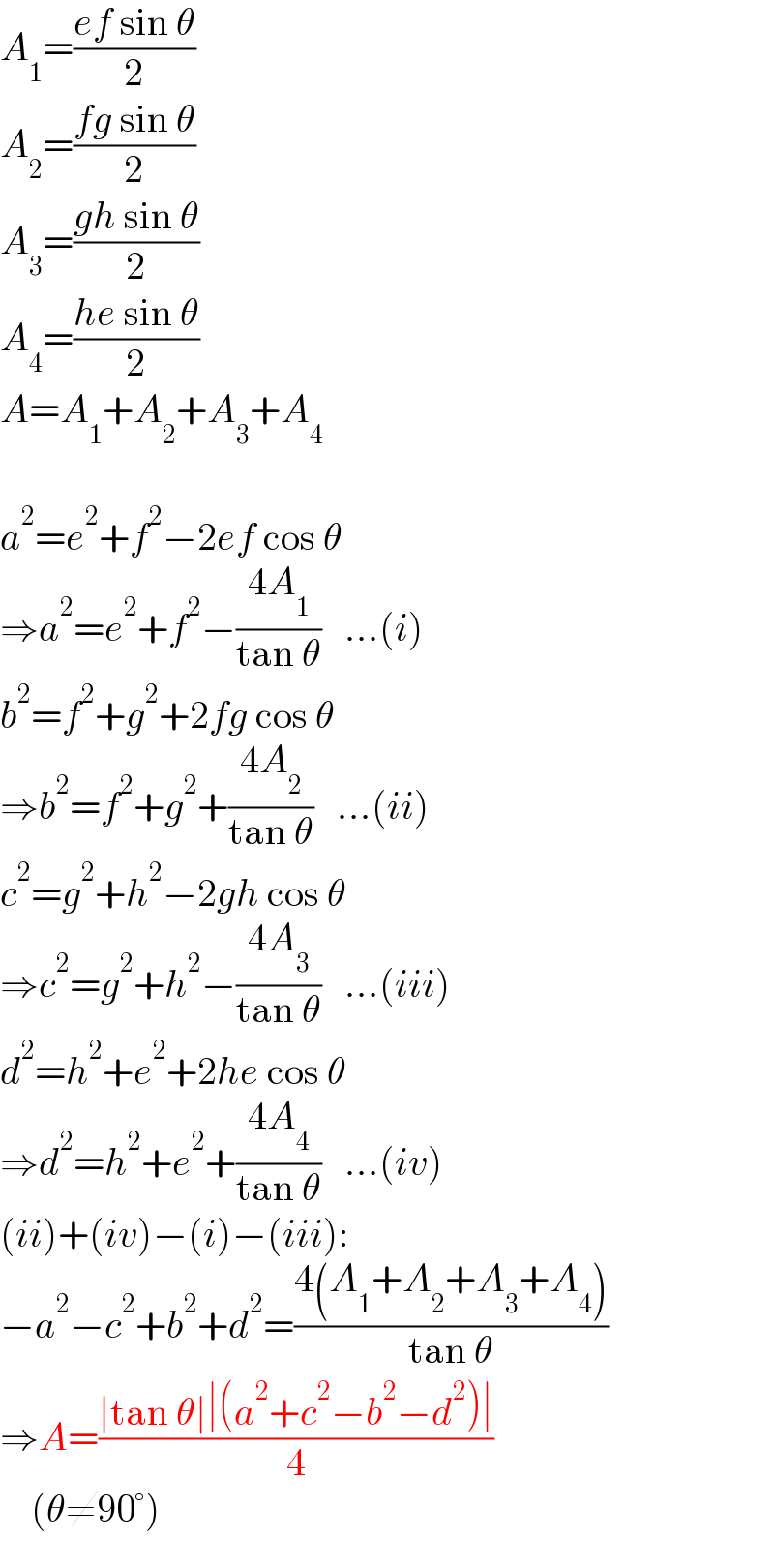
A_1 =((ef sin θ)/2) A_2 =((fg sin θ)/2) A_3 =((gh sin θ)/2) A_4 =((he sin θ)/2) A=A_1 +A_2 +A_3 +A_4 a^2 =e^2 +f^2 −2ef cos θ ⇒a^2 =e^2 +f^2 −((4A_1 )/(tan θ)) ...(i) b^2 =f^2 +g^2 +2fg cos θ ⇒b^2 =f^2 +g^2 +((4A_2 )/(tan θ)) ...(ii) c^2 =g^2 +h^2 −2gh cos θ ⇒c^2 =g^2 +h^2 −((4A_3 )/(tan θ)) ...(iii) d^2 =h^2 +e^2 +2he cos θ ⇒d^2 =h^2 +e^2 +((4A_4 )/(tan θ)) ...(iv) (ii)+(iv)−(i)−(iii): −a^2 −c^2 +b^2 +d^2 =((4(A_1 +A_2 +A_3 +A_4 ))/(tan θ)) ⇒A=((∣tan θ∣∣(a^2 +c^2 −b^2 −d^2 )∣)/4) (θ≠90°)

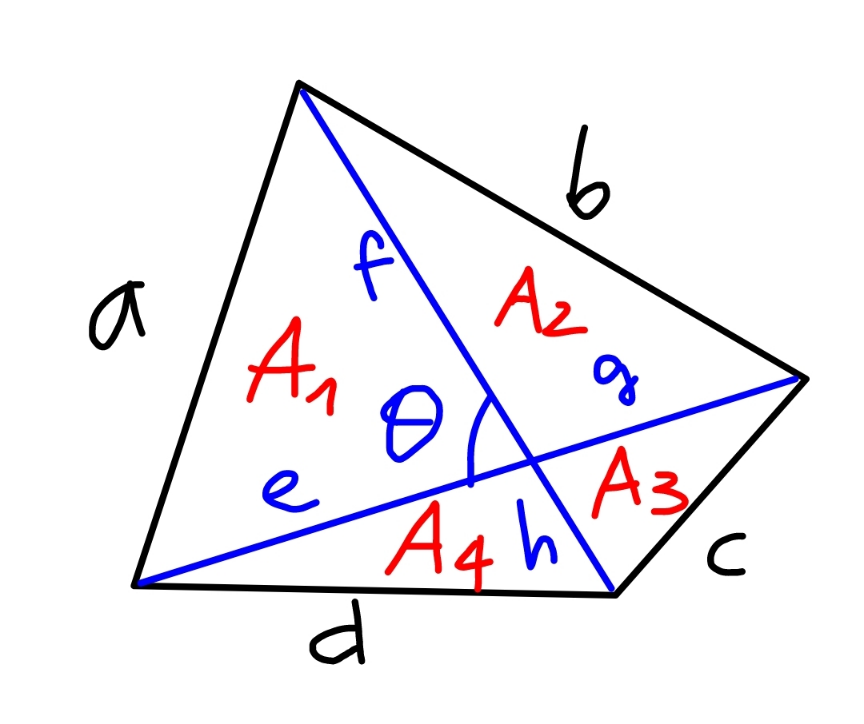
$${A}_{\mathrm{1}} =\frac{{ef}\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$${A}_{\mathrm{2}} =\frac{{fg}\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$${A}_{\mathrm{3}} =\frac{{gh}\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$${A}_{\mathrm{4}} =\frac{{he}\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$${A}={A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}_{\mathrm{3}} +{A}_{\mathrm{4}} \\ $$$$ \\ $$$${a}^{\mathrm{2}} ={e}^{\mathrm{2}} +{f}^{\mathrm{2}} −\mathrm{2}{ef}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{a}^{\mathrm{2}} ={e}^{\mathrm{2}} +{f}^{\mathrm{2}} −\frac{\mathrm{4}{A}_{\mathrm{1}} }{\mathrm{tan}\:\theta}\:\:\:…\left({i}\right) \\ $$$${b}^{\mathrm{2}} ={f}^{\mathrm{2}} +{g}^{\mathrm{2}} +\mathrm{2}{fg}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{b}^{\mathrm{2}} ={f}^{\mathrm{2}} +{g}^{\mathrm{2}} +\frac{\mathrm{4}{A}_{\mathrm{2}} }{\mathrm{tan}\:\theta}\:\:\:…\left({ii}\right) \\ $$$${c}^{\mathrm{2}} ={g}^{\mathrm{2}} +{h}^{\mathrm{2}} −\mathrm{2}{gh}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{c}^{\mathrm{2}} ={g}^{\mathrm{2}} +{h}^{\mathrm{2}} −\frac{\mathrm{4}{A}_{\mathrm{3}} }{\mathrm{tan}\:\theta}\:\:\:…\left({iii}\right) \\ $$$${d}^{\mathrm{2}} ={h}^{\mathrm{2}} +{e}^{\mathrm{2}} +\mathrm{2}{he}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{d}^{\mathrm{2}} ={h}^{\mathrm{2}} +{e}^{\mathrm{2}} +\frac{\mathrm{4}{A}_{\mathrm{4}} }{\mathrm{tan}\:\theta}\:\:\:…\left({iv}\right) \\ $$$$\left({ii}\right)+\left({iv}\right)−\left({i}\right)−\left({iii}\right): \\ $$$$−{a}^{\mathrm{2}} −{c}^{\mathrm{2}} +{b}^{\mathrm{2}} +{d}^{\mathrm{2}} =\frac{\mathrm{4}\left({A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}_{\mathrm{3}} +{A}_{\mathrm{4}} \right)}{\mathrm{tan}\:\theta} \\ $$$$\Rightarrow{A}=\frac{\mid\mathrm{tan}\:\theta\mid\mid\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)\mid}{\mathrm{4}} \\ $$$$\:\:\:\:\left(\theta\neq\mathrm{90}°\right) \\ $$

Commented by Matica last updated on 16/Sep/22

$${Thank}\:{you} \\ $$

Commented by Tawa11 last updated on 18/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply