Question Number 176316 by Matica last updated on 16/Sep/22

$$\:\:{xy}+{xz}=\mathrm{255} \\ $$$$\:{xz}−{yz}=\mathrm{224}. \\ $$$${find}\:{x}\:{y}\:{and}\:{z} \\ $$
Answered by Frix last updated on 16/Sep/22
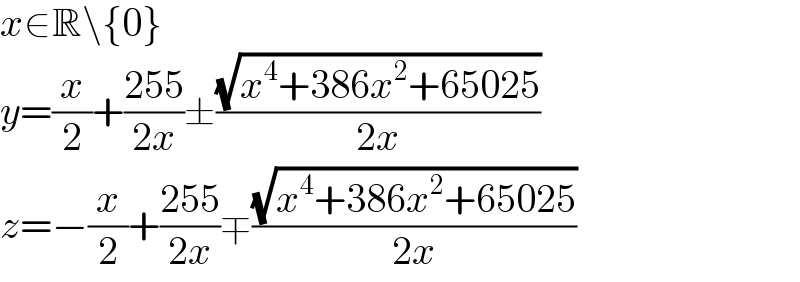
$${x}\in\mathbb{R}\backslash\left\{\mathrm{0}\right\} \\ $$$${y}=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{255}}{\mathrm{2}{x}}\pm\frac{\sqrt{{x}^{\mathrm{4}} +\mathrm{386}{x}^{\mathrm{2}} +\mathrm{65025}}}{\mathrm{2}{x}} \\ $$$${z}=−\frac{{x}}{\mathrm{2}}+\frac{\mathrm{255}}{\mathrm{2}{x}}\mp\frac{\sqrt{{x}^{\mathrm{4}} +\mathrm{386}{x}^{\mathrm{2}} +\mathrm{65025}}}{\mathrm{2}{x}} \\ $$
