Question Number 45410 by Rio Michael last updated on 12/Oct/18
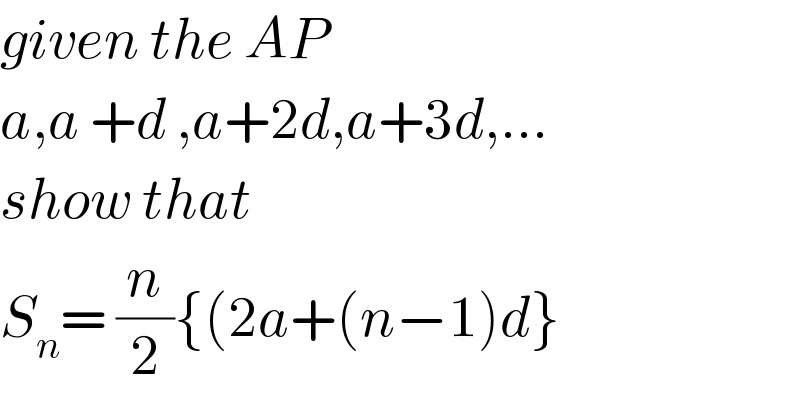
$${given}\:{the}\:{AP} \\ $$$${a},{a}\:+{d}\:,{a}+\mathrm{2}{d},{a}+\mathrm{3}{d},… \\ $$$${show}\:{that}\: \\ $$$${S}_{{n}} =\:\frac{{n}}{\mathrm{2}}\left\{\left(\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right\}\right. \\ $$
Commented by maxmathsup by imad last updated on 13/Oct/18
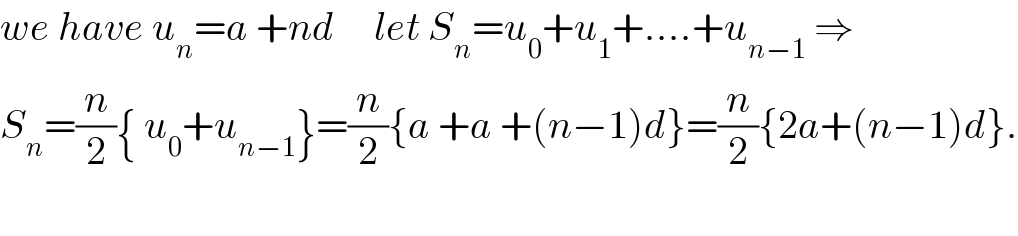
$${we}\:{have}\:{u}_{{n}} ={a}\:+{nd}\:\:\:\:\:{let}\:{S}_{{n}} ={u}_{\mathrm{0}} +{u}_{\mathrm{1}} +….+{u}_{{n}−\mathrm{1}} \:\Rightarrow \\ $$$${S}_{{n}} =\frac{{n}}{\mathrm{2}}\left\{\:{u}_{\mathrm{0}} +{u}_{{n}−\mathrm{1}} \right\}=\frac{{n}}{\mathrm{2}}\left\{{a}\:+{a}\:+\left({n}−\mathrm{1}\right){d}\right\}=\frac{{n}}{\mathrm{2}}\left\{\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right\}. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18
![S_n =a+(a+d)+(a+2d)+..+{a+(n−1)d} S_n ={a+(n−1)d}+{a+(n−2)d}+..+a add them 2S_n =[a+a+(n−1)d]+[a+d+a+(n−2)d]+.. 2S_n =[2a+(n−1)d]+[2a+(n−1)d]+..n terms 2S_n =n[2a+(n−1)d](.nterms) 2S_n =n[2a+(n−1)d] S_n =(n/2)[2a+(n−1)d]](https://www.tinkutara.com/question/Q45431.png)
$${S}_{{n}} ={a}+\left({a}+{d}\right)+\left({a}+\mathrm{2}{d}\right)+..+\left\{{a}+\left({n}−\mathrm{1}\right){d}\right\} \\ $$$${S}_{{n}} =\left\{{a}+\left({n}−\mathrm{1}\right){d}\right\}+\left\{{a}+\left({n}−\mathrm{2}\right){d}\right\}+..+{a} \\ $$$${add}\:{them} \\ $$$$\mathrm{2}{S}_{{n}} =\left[{a}+{a}+\left({n}−\mathrm{1}\right){d}\right]+\left[{a}+{d}+{a}+\left({n}−\mathrm{2}\right){d}\right]+.. \\ $$$$\mathrm{2}{S}_{{n}} =\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right]+\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right]+..{n}\:{terms} \\ $$$$\mathrm{2}{S}_{{n}} ={n}\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right]\left(.{nterms}\right) \\ $$$$\mathrm{2}{S}_{{n}} ={n}\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right] \\ $$$${S}_{{n}} =\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right] \\ $$$$ \\ $$
