Question Number 176555 by Shrinava last updated on 21/Sep/22

$$\mathrm{ABCD}−\mathrm{convex}\:\mathrm{quadrilateral} \\ $$$$\mathrm{M}\in\mathrm{Int}\left(\mathrm{ABCD}\right)\:,\:\mathrm{F}−\mathrm{area}\:,\:\mathrm{s}−\mathrm{semiperimetr} \\ $$$$\mathrm{a}\:,\:\mathrm{b}\:,\:\mathrm{c}−\mathrm{sides}.\:\mathrm{Prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{MA}^{\mathrm{4}} }{\mathrm{b}}\:+\:\frac{\mathrm{MB}^{\mathrm{4}} }{\mathrm{c}^{\mathrm{4}} }\:+\:\frac{\mathrm{MC}^{\mathrm{4}} }{\mathrm{d}}\:+\:\frac{\mathrm{MD}^{\mathrm{4}} }{\mathrm{a}}\:\geqslant\:\frac{\mathrm{2F}^{\mathrm{2}} }{\mathrm{s}} \\ $$
Commented by mr W last updated on 21/Sep/22
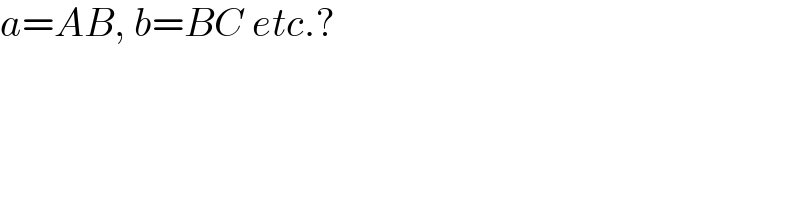
$${a}={AB},\:{b}={BC}\:{etc}.? \\ $$
Commented by Shrinava last updated on 21/Sep/22
$$\mathrm{yes}\:\mathrm{dear}\:\mathrm{professor} \\ $$
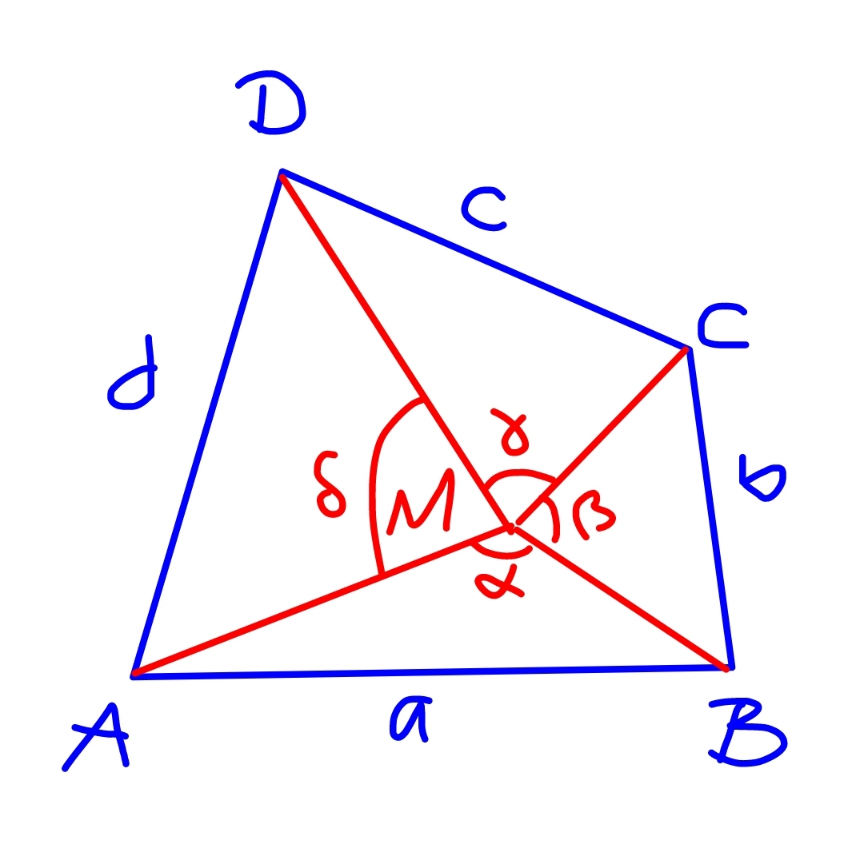
Answered by mr W last updated on 24/Sep/22
Commented by Shrinava last updated on 27/Sep/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$$$\mathrm{so}\:\mathrm{that}'\mathrm{s}\:\mathrm{it}? \\ $$
Commented by mr W last updated on 04/Oct/22

$${s}=\frac{{a}+{b}+{c}+{d}}{\mathrm{2}} \\ $$$${F}=\frac{{MA}×{MB}×\mathrm{sin}\:\alpha}{\mathrm{2}}+\frac{{MB}×{MC}×\mathrm{sin}\:\beta}{\mathrm{2}}+\frac{{MC}×{MD}×\mathrm{sin}\:\gamma}{\mathrm{2}}+\frac{{MD}×{MA}×\mathrm{sin}\:\delta}{\mathrm{2}} \\ $$$$\:\:\:\leqslant\frac{\mathrm{1}}{\mathrm{2}}\left({MA}×{MB}+{MB}×{MC}+{MC}×{MD}+{MD}×{MA}\right) \\ $$$$\:\:\:\leqslant\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{MA}^{\mathrm{2}} +{MB}^{\mathrm{2}} }{\mathrm{2}}+\frac{{MB}^{\mathrm{2}} +{MC}^{\mathrm{2}} }{\mathrm{2}}+\frac{{MC}^{\mathrm{2}} +{MD}^{\mathrm{2}} }{\mathrm{2}}+\frac{{MD}^{\mathrm{2}} +{MA}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\:\:\:=\frac{{MA}^{\mathrm{2}} +{MB}^{\mathrm{2}} +{MC}^{\mathrm{2}} +{MD}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{\mathrm{2}{F}^{\mathrm{2}} }{{s}}\leqslant\frac{\left({MA}^{\mathrm{2}} +{MB}^{\mathrm{2}} +{MC}^{\mathrm{2}} +{MD}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}+{b}+{c}+{d}} \\ $$$$\left.\:\:\:\:\:\:\:\leqslant\frac{{MA}^{\mathrm{4}} }{{b}}+\frac{{MB}^{\mathrm{4}} }{{c}}+\frac{{MC}^{\mathrm{4}} }{{d}}+\frac{{MD}^{\mathrm{4}} }{{a}}\:\:\:\:\:\:\ast\right) \\ $$$$\:\:\:\:\:\:\:{proved}!\:\checkmark \\ $$$$ \\ $$$$\left.\ast\right)\:\:{see}\:{Chaucy}−{Schwarz}\:{Inequality} \\ $$
Commented by Shrinava last updated on 24/Sep/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{please} \\ $$
Commented by mr W last updated on 04/Oct/22
$${yes}.\:{now}\:{the}\:{proof}\:{is}\:{complete}. \\ $$
Commented by mr W last updated on 04/Oct/22
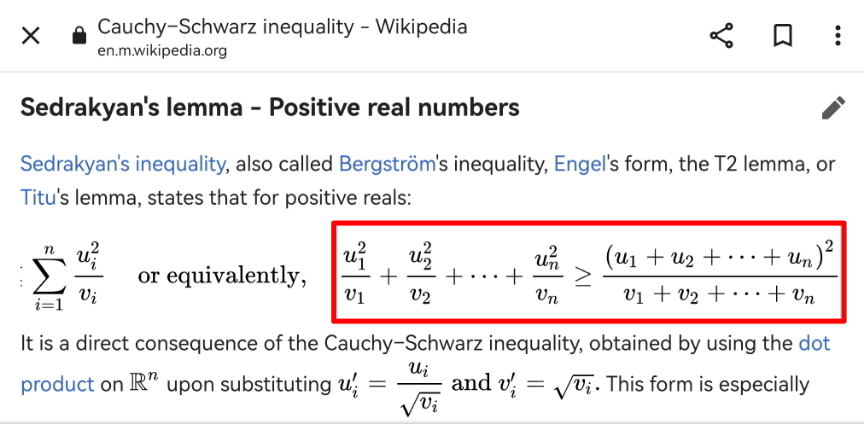
Commented by Shrinava last updated on 08/Oct/22
$$\mathrm{perfect}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
