Question Number 111218 by Lekhraj last updated on 02/Sep/20
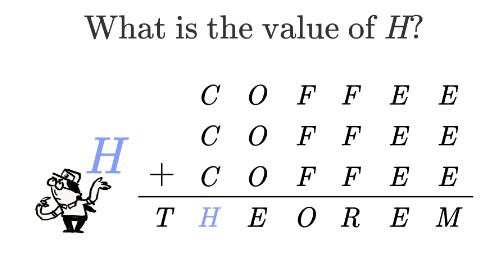
Answered by nimnim last updated on 02/Sep/20

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{9}\:\:\:\:\:\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{9}\:\:\:\:\:\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\mathrm{8}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{9}\:\:\:\:\:\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{4}\:\:\:\:\:\mathrm{9}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{5}\:\:\:\:\mathrm{9}\:\:\:\:\:\mathrm{7} \\ $$$$ \\ $$$$\:\:\therefore\:\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:{H}\:\mathrm{is}\:\mathrm{4}\:\bigstar \\ $$
Commented by Rasheed.Sindhi last updated on 03/Sep/20
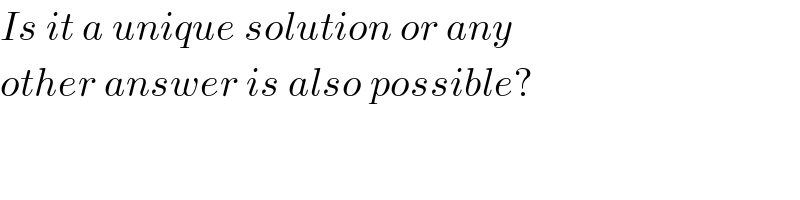
$${Is}\:{it}\:{a}\:{unique}\:{solution}\:{or}\:{any} \\ $$$${other}\:{answer}\:{is}\:{also}\:{possible}? \\ $$
Commented by Lekhraj last updated on 03/Sep/20
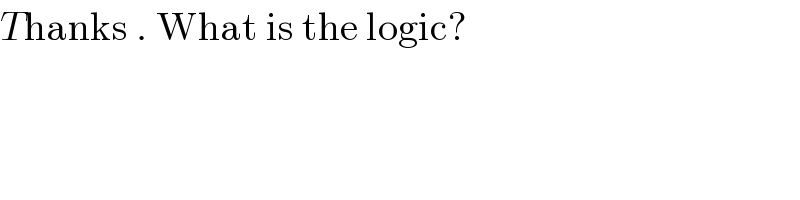
$${T}\mathrm{hanks}\:.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{logic}? \\ $$
Commented by Rasheed.Sindhi last updated on 03/Sep/20

$${Nice}\:{approach}! \\ $$
Commented by nimnim last updated on 03/Sep/20
![[( ,C,O,F,F,E,E),( ,C,O,F,F,E,E),(+,C,O,F,F,E,E),(T,H,E,O,R,E,M) ] 3E=10a+M and 3E=10b+E the only possibility is E=9,a=b=2, then we have [( ,C,O,F,F^(+2) ,9,9),( ,C,O,F,F,9,9),(+,C,O,F,F,9,9),(T,H,9,O,R,9,7) ] 3O=9, 3F gives carry 0,1,2 ∴ 3O+c=9 where c=0,1,2 ⇒O=3. only c=0 gives integer. then we have [( ,C,3,F,F^(+2) ,9,9),( ,C,3,F,F,9,9),(+,C,3,F,F,9,9),(T,H,9,3,R,9,7) ] so,3F=3⇒F=1,then R=5 since T≠F=1 and 3C=TH ⇒T=2 and 3C=20+H (C>6) ∴ C=8⇒H=4 [( ,8,3,1,1,9,9),( ,8,3,1,1,9,9),(+,8,3,1,1,9,9),(2,4,9,3,5,9,7) ] There might be other method. This is how it pop up in my head. Thank you. ≻NimNim≺](https://www.tinkutara.com/question/Q111464.png)
$$\:\:\:\:\:\:\begin{bmatrix}{\:}&{\mathrm{C}}&{\mathrm{O}}&{\mathrm{F}}&{\mathrm{F}}&{\mathrm{E}}&{\mathrm{E}}\\{\:}&{\mathrm{C}}&{\mathrm{O}}&{\mathrm{F}}&{\mathrm{F}}&{\mathrm{E}}&{\mathrm{E}}\\{+}&{\mathrm{C}}&{\mathrm{O}}&{\mathrm{F}}&{\mathrm{F}}&{\mathrm{E}}&{\mathrm{E}}\\{\mathrm{T}}&{\mathrm{H}}&{\mathrm{E}}&{\mathrm{O}}&{\mathrm{R}}&{\mathrm{E}}&{\mathrm{M}}\end{bmatrix} \\ $$$$\mathrm{3E}=\mathrm{10a}+\mathrm{M}\:\mathrm{and}\:\mathrm{3E}=\mathrm{10b}+\mathrm{E} \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{possibility}\:\mathrm{is} \\ $$$$\mathrm{E}=\mathrm{9},\mathrm{a}=\mathrm{b}=\mathrm{2},\:\mathrm{then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\:\:\:\:\:\:\begin{bmatrix}{\:}&{\mathrm{C}}&{\mathrm{O}}&{\mathrm{F}}&{\overset{+\mathrm{2}} {\mathrm{F}}}&{\mathrm{9}}&{\mathrm{9}}\\{\:}&{\mathrm{C}}&{\mathrm{O}}&{\mathrm{F}}&{\mathrm{F}}&{\mathrm{9}}&{\mathrm{9}}\\{+}&{\mathrm{C}}&{\mathrm{O}}&{\mathrm{F}}&{\mathrm{F}}&{\mathrm{9}}&{\mathrm{9}}\\{\mathrm{T}}&{\mathrm{H}}&{\mathrm{9}}&{\mathrm{O}}&{\mathrm{R}}&{\mathrm{9}}&{\mathrm{7}}\end{bmatrix} \\ $$$$\mathrm{3O}=\mathrm{9},\:\mathrm{3F}\:\mathrm{gives}\:\mathrm{carry}\:\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$\therefore\:\mathrm{3O}+\mathrm{c}=\mathrm{9}\:\mathrm{where}\:\mathrm{c}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$\Rightarrow\mathrm{O}=\mathrm{3}.\:\mathrm{only}\:\mathrm{c}=\mathrm{0}\:\mathrm{gives}\:\mathrm{integer}. \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\:\:\:\:\:\:\begin{bmatrix}{\:}&{\mathrm{C}}&{\mathrm{3}}&{\mathrm{F}}&{\overset{+\mathrm{2}} {\mathrm{F}}}&{\mathrm{9}}&{\mathrm{9}}\\{\:}&{\mathrm{C}}&{\mathrm{3}}&{\mathrm{F}}&{\mathrm{F}}&{\mathrm{9}}&{\mathrm{9}}\\{+}&{\mathrm{C}}&{\mathrm{3}}&{\mathrm{F}}&{\mathrm{F}}&{\mathrm{9}}&{\mathrm{9}}\\{\mathrm{T}}&{\mathrm{H}}&{\mathrm{9}}&{\mathrm{3}}&{\mathrm{R}}&{\mathrm{9}}&{\mathrm{7}}\end{bmatrix} \\ $$$$\:\:\:\:\:\: \\ $$$$\:\mathrm{so},\mathrm{3F}=\mathrm{3}\Rightarrow\mathrm{F}=\mathrm{1},\mathrm{then}\:\mathrm{R}=\mathrm{5} \\ $$$$\mathrm{since}\:\mathrm{T}\neq\mathrm{F}=\mathrm{1}\:\mathrm{and}\:\mathrm{3C}=\mathrm{TH} \\ $$$$\Rightarrow\mathrm{T}=\mathrm{2}\:\mathrm{and}\:\mathrm{3C}=\mathrm{20}+\mathrm{H}\:\left(\mathrm{C}>\mathrm{6}\right) \\ $$$$\therefore\:\mathrm{C}=\mathrm{8}\Rightarrow\mathrm{H}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\begin{bmatrix}{\:}&{\mathrm{8}}&{\mathrm{3}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{9}}&{\mathrm{9}}\\{\:}&{\mathrm{8}}&{\mathrm{3}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{9}}&{\mathrm{9}}\\{+}&{\mathrm{8}}&{\mathrm{3}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{9}}&{\mathrm{9}}\\{\mathrm{2}}&{\mathrm{4}}&{\mathrm{9}}&{\mathrm{3}}&{\mathrm{5}}&{\mathrm{9}}&{\mathrm{7}}\end{bmatrix} \\ $$$$\:\mathrm{There}\:\mathrm{might}\:\mathrm{be}\:\mathrm{other}\:\mathrm{method}. \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{how}\:\mathrm{it}\:\mathrm{pop}\:\mathrm{up}\:\mathrm{in}\:\mathrm{my}\:\mathrm{head}. \\ $$$$\:\:\:\:\:\:\mathrm{Thank}\:\mathrm{you}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\succ\mathrm{NimNim}\prec \\ $$
Commented by nimnim last updated on 03/Sep/20

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}. \\ $$$$ \\ $$
