Question Number 135627 by mnjuly1970 last updated on 14/Mar/21

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:……………..\:{calculus}\:… \\ $$$$\:\:\:\:\:\:\:{evaluation}:::::\:\:\:\boldsymbol{\phi}\overset{???} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}\left({x}\right){ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:\:\:{solution}::::: \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}\overset{\langle{cos}\left({x}\right)={y}\rangle} {=}\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\mathrm{1}−{y}^{\mathrm{2}} \right){dy} \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \underset{{n}=\mathrm{1}\:\:} {\overset{\infty} {\sum}}\frac{{y}^{\mathrm{2}{n}} }{{n}}=\frac{−\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {y}^{\mathrm{2}{n}} {dy}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{−\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)}=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:=−\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}}+…\right) \\ $$$$\:\:\:\:\:\:\:\:\:=−\mathrm{1}+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−…\right) \\ $$$$\:\:\:\:\:\:\:\:\:=−\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\underset{{harmonic}\:{seties}} {\overset{{alternating}} {=}}−\mathrm{1}+{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\phi}=\:−\mathrm{1}+{ln}\left(\mathrm{2}\right)={ln}\left(\frac{\mathrm{2}}{{e}}\right) \\ $$$$\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 14/Mar/21
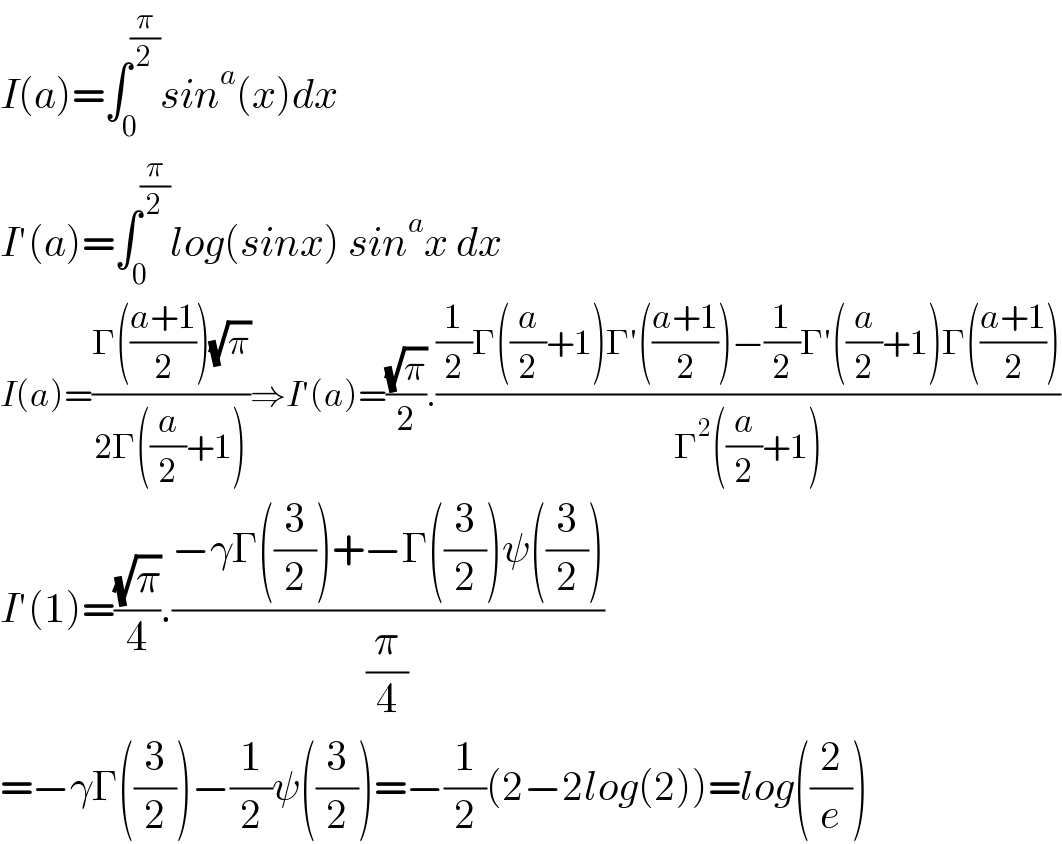
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{{a}} \left({x}\right){dx} \\ $$$${I}'\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sinx}\right)\:{sin}^{{a}} {x}\:{dx} \\ $$$${I}\left({a}\right)=\frac{\Gamma\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)\sqrt{\pi}}{\mathrm{2}\Gamma\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)}\Rightarrow{I}'\left({a}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}.\frac{\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)\Gamma'\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\Gamma'\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)\Gamma\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)}{\Gamma^{\mathrm{2}} \left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$${I}'\left(\mathrm{1}\right)=\frac{\sqrt{\pi}}{\mathrm{4}}.\frac{−\gamma\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+−\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\frac{\pi}{\mathrm{4}}} \\ $$$$=−\gamma\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}−\mathrm{2}{log}\left(\mathrm{2}\right)\right)={log}\left(\frac{\mathrm{2}}{{e}}\right) \\ $$
