Question Number 111340 by ajfour last updated on 03/Sep/20
Commented by ajfour last updated on 03/Sep/20

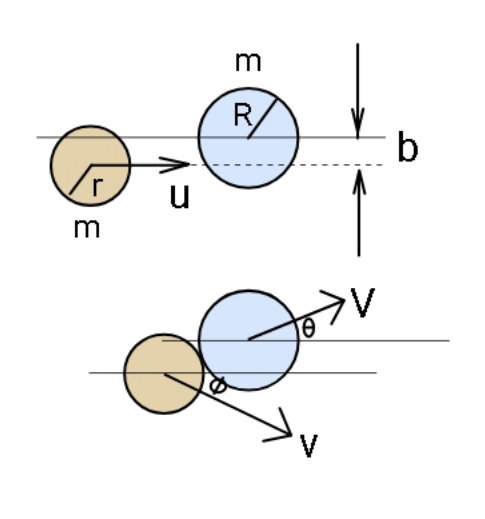
$${Diagrams}\:{show}\:{collision}\:{of}\:{two}\:{balls}\: \\ $$$${on}\:{flat}\:{frictionless}\:{surface}\:{before} \\ $$$${collision}\:{and}\:{just}\:{after}\:{collision}. \\ $$$${coefficient}\:{of}\:{restitution}\:{being}\:\boldsymbol{{e}}. \\ $$$${Find}\:{v},\:{V},\:\theta,\:\phi\:\:{in}\:{terms}\:{of}\: \\ $$$${u},\:{b},\:\:{r},\:{R},\:{and}\:{e}. \\ $$
Commented by ajfour last updated on 04/Sep/20
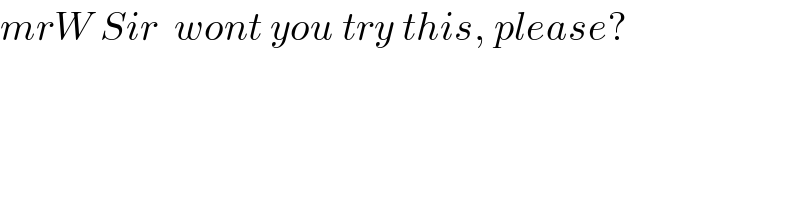
$${mrW}\:{Sir}\:\:{wont}\:{you}\:{try}\:{this},\:{please}? \\ $$
Answered by mr W last updated on 15/Sep/20
![μ=(M/m) sin θ=(b/(r+R)) V−v cos (θ+φ)=e u cos θ ⇒V=v cos (θ+φ)+eu cos θ mu cos θ=M V+mv cos (θ+φ) ⇒u cos θ=μV+v cos (θ+φ) mu sin θ=m v sin (θ+φ) ⇒u sin θ=v sin (θ+φ) ⇒(v/u)=(1/(cos φ+((sin φ)/(tan θ)))) u cos θ=μv cos (θ+φ)+μeu cos θ+v cos (θ+φ) ⇒(1−μe)=(v/u)(1+μ)(cos φ−tan θ sin φ) ⇒((1−μe)/(1+μ))=((cos φ−tan θ sin φ)/(cos φ+((sin φ)/(tan θ)))) ⇒((1−μe)/(1+μ))=((1−tan θ tan φ)/(1+((tan φ)/(tan θ)))) ⇒[tan θ+((1−μe)/((1+μ)tan θ))]tan φ=((μ(1+e))/(1+μ)) ⇒tan φ=((μ(1+e))/((1+μ)tan θ+((1−μe)/(tan θ))))](https://www.tinkutara.com/question/Q113844.png)
$$\mu=\frac{{M}}{{m}} \\ $$$$\mathrm{sin}\:\theta=\frac{{b}}{{r}+{R}} \\ $$$${V}−{v}\:\mathrm{cos}\:\left(\theta+\phi\right)={e}\:{u}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{V}={v}\:\mathrm{cos}\:\left(\theta+\phi\right)+{eu}\:\mathrm{cos}\:\theta \\ $$$${mu}\:\mathrm{cos}\:\theta={M}\:{V}+{mv}\:\mathrm{cos}\:\left(\theta+\phi\right) \\ $$$$\Rightarrow{u}\:\mathrm{cos}\:\theta=\mu{V}+{v}\:\mathrm{cos}\:\left(\theta+\phi\right) \\ $$$${mu}\:\mathrm{sin}\:\theta={m}\:{v}\:\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$$\Rightarrow{u}\:\mathrm{sin}\:\theta={v}\:\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$$\Rightarrow\frac{{v}}{{u}}=\frac{\mathrm{1}}{\mathrm{cos}\:\phi+\frac{\mathrm{sin}\:\phi}{\mathrm{tan}\:\theta}} \\ $$$${u}\:\mathrm{cos}\:\theta=\mu{v}\:\mathrm{cos}\:\left(\theta+\phi\right)+\mu{eu}\:\mathrm{cos}\:\theta+{v}\:\mathrm{cos}\:\left(\theta+\phi\right) \\ $$$$\Rightarrow\left(\mathrm{1}−\mu{e}\right)=\frac{{v}}{{u}}\left(\mathrm{1}+\mu\right)\left(\mathrm{cos}\:\phi−\mathrm{tan}\:\theta\:\mathrm{sin}\:\phi\right) \\ $$$$\Rightarrow\frac{\mathrm{1}−\mu{e}}{\mathrm{1}+\mu}=\frac{\mathrm{cos}\:\phi−\mathrm{tan}\:\theta\:\mathrm{sin}\:\phi}{\mathrm{cos}\:\phi+\frac{\mathrm{sin}\:\phi}{\mathrm{tan}\:\theta}} \\ $$$$\Rightarrow\frac{\mathrm{1}−\mu{e}}{\mathrm{1}+\mu}=\frac{\mathrm{1}−\mathrm{tan}\:\theta\:\mathrm{tan}\:\phi}{\mathrm{1}+\frac{\mathrm{tan}\:\phi}{\mathrm{tan}\:\theta}} \\ $$$$\Rightarrow\left[\mathrm{tan}\:\theta+\frac{\mathrm{1}−\mu{e}}{\left(\mathrm{1}+\mu\right)\mathrm{tan}\:\theta}\right]\mathrm{tan}\:\phi=\frac{\mu\left(\mathrm{1}+{e}\right)}{\mathrm{1}+\mu} \\ $$$$\Rightarrow\mathrm{tan}\:\phi=\frac{\mu\left(\mathrm{1}+{e}\right)}{\left(\mathrm{1}+\mu\right)\mathrm{tan}\:\theta+\frac{\mathrm{1}−\mu{e}}{\mathrm{tan}\:\theta}} \\ $$
Commented by ajfour last updated on 23/Sep/20

$${thanks}\:{Sir}! \\ $$
