Question Number 45896 by Sanjarbek last updated on 18/Oct/18

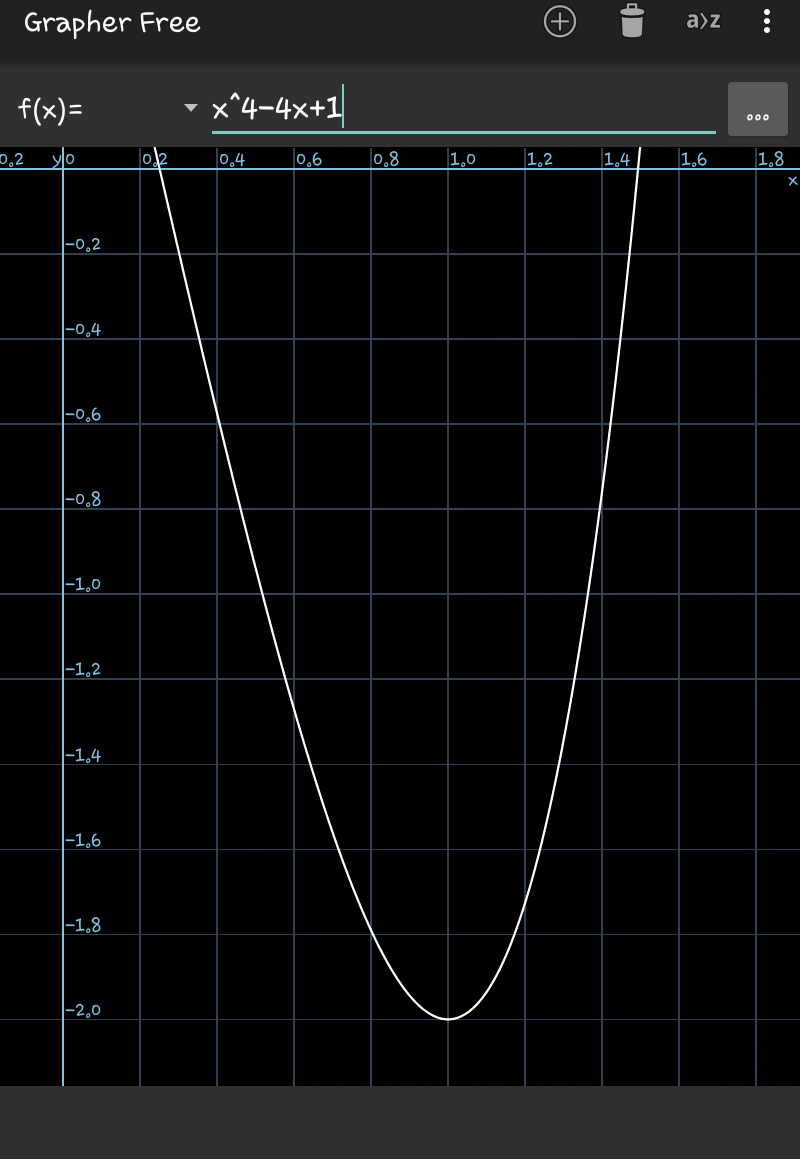
$$\boldsymbol{{solve}}\:\boldsymbol{{for}}\:\boldsymbol{{x}} \\ $$$$\boldsymbol{{x}}^{\mathrm{4}} −\mathrm{4}\boldsymbol{{x}}+\mathrm{1}=\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 18/Oct/18
Commented by tanmay.chaudhury50@gmail.com last updated on 18/Oct/18
Answered by ajfour last updated on 19/Oct/18

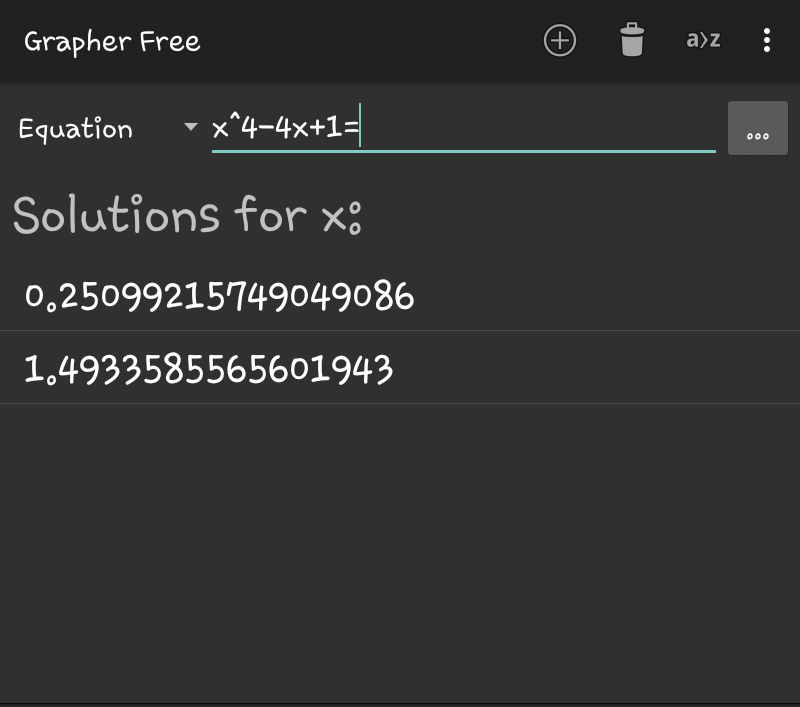
$${let}\:\:{x}^{\mathrm{4}} −\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\:\Leftrightarrow\:\left({x}^{\mathrm{2}} +{ax}+{b}\right)\left({x}^{\mathrm{2}} −{ax}+\frac{\mathrm{1}}{{b}}\right)=\mathrm{0} \\ $$$$\:\:\Leftrightarrow\:{x}^{\mathrm{4}} +\left({b}+\frac{\mathrm{1}}{{b}}−{a}^{\mathrm{2}} \right){x}^{\mathrm{2}} +{a}\left(\frac{\mathrm{1}}{{b}}−{b}\right){x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{{b}}+{b}\:=\:{a}^{\mathrm{2}} \:\:;\:\:\:\frac{\mathrm{1}}{{b}}−{b}\:=\:−\frac{\mathrm{4}}{{a}} \\ $$$${adding}:\:\:\:\:\:\:{a}^{\mathrm{2}} −\frac{\mathrm{4}}{{a}}=\:\frac{\mathrm{2}}{{b}}\:\:\:\:\:…\left({i}\right) \\ $$$${subtracting}:\:\:\:{a}^{\mathrm{2}} +\frac{\mathrm{4}}{{a}}\:=\:\mathrm{2}{b}\:\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:\:\:\:{b}\:>\:\mathrm{0}\:\: \\ $$$${multiplying}\:{above}\:{two}\:{eqs}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{4}} −\frac{\mathrm{16}}{{a}^{\mathrm{2}} }\:=\mathrm{4} \\ $$$${let}\:\:{s}\:=\:{a}^{\mathrm{2}} \:,\:{then} \\ $$$$\:\:\:\:\:\:\:{s}^{\mathrm{3}} −\mathrm{4}{s}−\mathrm{16}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{s}={a}^{\mathrm{2}} =\:\left(\mathrm{8}+\frac{\mathrm{8}}{\mathrm{3}}\sqrt{\frac{\mathrm{26}}{\mathrm{3}}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{8}−\frac{\mathrm{8}}{\mathrm{3}}\sqrt{\frac{\mathrm{26}}{\mathrm{3}}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:{a}^{\mathrm{2}} \approx\:\mathrm{3}.\mathrm{04275941} \\ $$$$\:\:\:\:{a}\:\approx\:\pm\mathrm{1}.\mathrm{74435071} \\ $$$$\:\:\:\:{b}\:=\:\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{2}}{{a}}\: \\ $$$$\:\:{with}\:+{ve}\:{a},\:\:{b}_{\mathrm{1}} \approx\:\mathrm{2}.\mathrm{66793813} \\ $$$$\:\:{with}\:−{ve}\:{a},\:\:{b}_{\mathrm{2}} \approx\:\mathrm{0}.\mathrm{374821282} \\ $$$${both}\:{sets}\:{satisfy}\:{eqs}.\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:\:{For}\:+{ve}\:\boldsymbol{{a}}\:\&\:{b}_{\mathrm{1}} \\ $$$$\:\:\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{ax}}+\boldsymbol{{b}}=\mathrm{0}\:\:{provides} \\ $$$$\:\:\:\:{x}=−\frac{{a}}{\mathrm{2}}\pm\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−{b}} \\ $$$$\:\:\:\:\:{no}\:{real}\:{roots};\:{while} \\ $$$$\:\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{ax}}+\mathrm{1}/\boldsymbol{{b}}\:=\mathrm{0}\:\:\:{gives} \\ $$$$\:\:\:\:{x}\:\approx\:−\mathrm{1}.\mathrm{49336}\:,\:−\mathrm{0}.\mathrm{25099} \\ $$$$\:{For}\:\:−{ve}\:\boldsymbol{{a}}\:\&\:{b}_{\mathrm{2}} \\ $$$$\:\:\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{ax}}+\boldsymbol{{b}}\:=\:\mathrm{0}\:\:\:{gives} \\ $$$$\:\:\:\:{x}\:\approx\:\mathrm{0}.\mathrm{25099}\:,\:\mathrm{1}.\mathrm{49336} \\ $$$$\:\:{while}\:\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{ax}}+\mathrm{1}/\boldsymbol{{b}}\:=\mathrm{0}\:\:{gives} \\ $$$$\:\:\:{no}\:{real}\:{roots}. \\ $$$${But}\:\:\:\frac{{d}}{{dx}}\left({x}^{\mathrm{4}} −\mathrm{4}{x}+\mathrm{1}\right)=\:\mathrm{4}{x}^{\mathrm{3}} −\mathrm{4} \\ $$$$\Rightarrow\:\:\frac{{dy}}{{dx}}=\mathrm{0}\:\:{only}\:{at}\:{x}=\mathrm{1} \\ $$$${so}\:{one}\:{root}\:{is}\:{certainly}\:>\:\mathrm{1} \\ $$$$\Rightarrow\:{we}\:{need}\:{to}\:{reject}\:{the}\:{negative} \\ $$$${set}\:{of}\:{roots};\:\:{the}\:{answer}\:{is}\:{indeed} \\ $$$$\:\:\:\:\:{x}_{\mathrm{1}} \approx\:\mathrm{0}.\mathrm{25099}\:\:\&\:\:{x}_{\mathrm{2}} \approx\:\mathrm{1}.\mathrm{49336}\:\:. \\ $$$$ \\ $$
Commented by peter frank last updated on 18/Oct/18

$$\mathrm{second}\:\mathrm{line}\:\mathrm{sir}\:\mathrm{clarify}\:\mathrm{plz} \\ $$$$ \\ $$
Commented by ajfour last updated on 18/Oct/18

$${coeff}.\:{of}\:{x}^{\mathrm{3}} \:{is}\:\mathrm{0}\:{and}\:{constant} \\ $$$${term}\:{is}\:\mathrm{1},\:{and}\:{i}\:{assumed}\:{a}\:{degree}\:\mathrm{4} \\ $$$${expression}\:{as}\:{a}\:{product}\:{of}\:{two} \\ $$$${quadratic}\:{expressions}.. \\ $$
Commented by peter frank last updated on 20/Oct/18
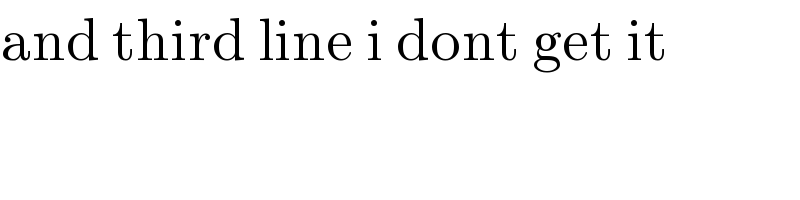
$$\mathrm{and}\:\mathrm{third}\:\mathrm{line}\:\mathrm{i}\:\mathrm{dont}\:\mathrm{get}\:\mathrm{it} \\ $$
Commented by ajfour last updated on 20/Oct/18
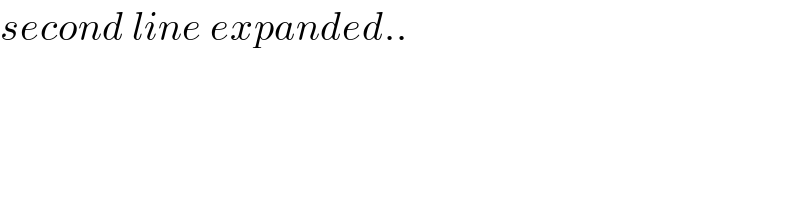
$${second}\:{line}\:{expanded}.. \\ $$
Commented by peter frank last updated on 20/Oct/18

$$\mathrm{thanks} \\ $$
Answered by mondodotto@gmail.com last updated on 18/Oct/18

