Question-45898

Question Number 45898 by rahul 19 last updated on 18/Oct/18

Commented by rahul 19 last updated on 18/Oct/18

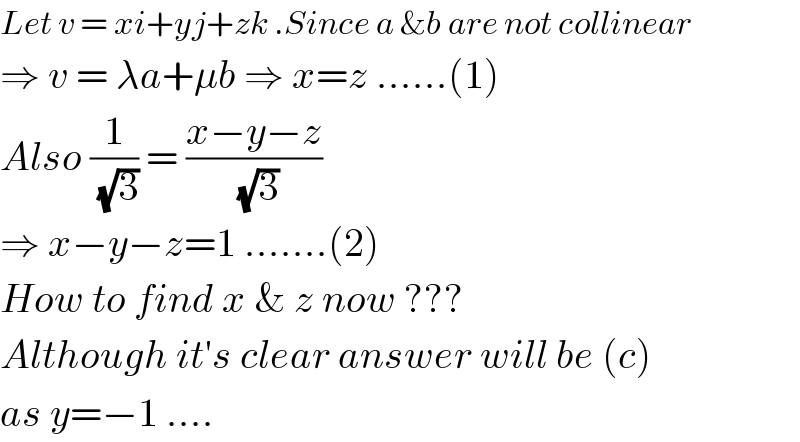
Let v = xi+yj+zk .Since a &b are not collinear ⇒ v = λa+μb ⇒ x=z ......(1) Also (1/( (√3))) = ((x−y−z)/( (√3))) ⇒ x−y−z=1 .......(2) How to find x & z now ??? Although it′s clear answer will be (c) as y=−1 ....

$${Let}\:{v}\:=\:{xi}+{yj}+{zk}\:.{Since}\:{a}\:\&{b}\:{are}\:{not}\:{collinear} \\ $$$$\Rightarrow\:{v}\:=\:\lambda{a}+\mu{b}\:\Rightarrow\:{x}={z}\:……\left(\mathrm{1}\right) \\ $$$${Also}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:=\:\frac{{x}−{y}−{z}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:{x}−{y}−{z}=\mathrm{1}\:…….\left(\mathrm{2}\right) \\ $$$${How}\:{to}\:{find}\:{x}\:\&\:{z}\:{now}\:??? \\ $$$${Although}\:{it}'{s}\:{clear}\:{answer}\:{will}\:{be}\:\left({c}\right) \\ $$$${as}\:{y}=−\mathrm{1}\:…. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 18/Oct/18

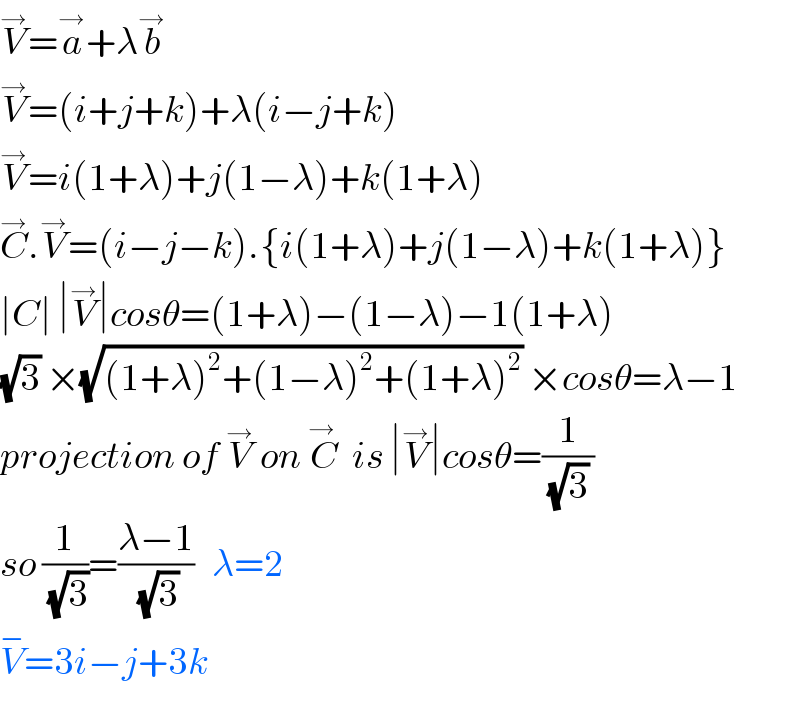
V^→ =a^→ +λb^→ V^→ =(i+j+k)+λ(i−j+k) V^→ =i(1+λ)+j(1−λ)+k(1+λ) C^→ .V^→ =(i−j−k).{i(1+λ)+j(1−λ)+k(1+λ)} ∣C∣ ∣V^→ ∣cosθ=(1+λ)−(1−λ)−1(1+λ) (√3) ×(√((1+λ)^2 +(1−λ)^2 +(1+λ)^2 )) ×cosθ=λ−1 projection of V^→ on C^(→ ) is ∣V^→ ∣cosθ=(1/( (√3) )) so (1/( (√3)))=((λ−1)/( (√3))) λ=2 V^− =3i−j+3k

$$\overset{\rightarrow} {{V}}=\overset{\rightarrow} {{a}}+\lambda\overset{\rightarrow} {{b}} \\ $$$$\overset{\rightarrow} {{V}}=\left({i}+{j}+{k}\right)+\lambda\left({i}−{j}+{k}\right) \\ $$$$\overset{\rightarrow} {{V}}={i}\left(\mathrm{1}+\lambda\right)+{j}\left(\mathrm{1}−\lambda\right)+{k}\left(\mathrm{1}+\lambda\right) \\ $$$$\overset{\rightarrow} {{C}}.\overset{\rightarrow} {{V}}=\left({i}−{j}−{k}\right).\left\{{i}\left(\mathrm{1}+\lambda\right)+{j}\left(\mathrm{1}−\lambda\right)+{k}\left(\mathrm{1}+\lambda\right)\right\} \\ $$$$\mid{C}\mid\:\mid\overset{\rightarrow} {{V}}\mid{cos}\theta=\left(\mathrm{1}+\lambda\right)−\left(\mathrm{1}−\lambda\right)−\mathrm{1}\left(\mathrm{1}+\lambda\right) \\ $$$$\sqrt{\mathrm{3}}\:×\sqrt{\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} +\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} +\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} }\:×{cos}\theta=\lambda−\mathrm{1} \\ $$$${projection}\:{of}\:\overset{\rightarrow} {{V}}\:{on}\:\overset{\rightarrow\:} {{C}}\:\:{is}\:\mid\overset{\rightarrow} {{V}}\mid{cos}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\:} \\ $$$${so}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\frac{\lambda−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\:\:\lambda=\mathrm{2} \\ $$$$\overset{−} {{V}}=\mathrm{3}{i}−{j}+\mathrm{3}{k} \\ $$

Commented by rahul 19 last updated on 18/Oct/18

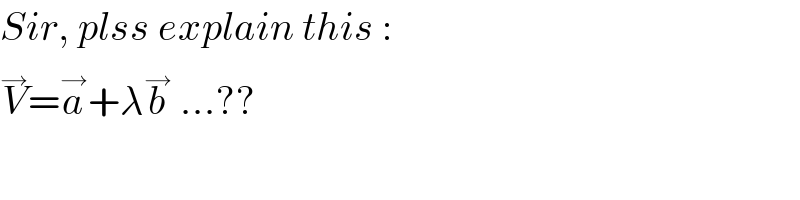
Sir, plss explain this : V^→ =a^→ +λb^→ ...??

$${Sir},\:{plss}\:{explain}\:{this}\:: \\ $$$$\overset{\rightarrow} {{V}}=\overset{\rightarrow} {{a}}+\lambda\overset{\rightarrow} {{b}}\:…?? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply