Question Number 65919 by mathmax by abdo last updated on 05/Aug/19

$${find}\:\:\int\:\:\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}\:+\left({x}+\mathrm{1}\right)\sqrt{{x}}} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}\:+\left({x}+\mathrm{1}\right)\sqrt{{x}}} \\ $$
Commented by mathmax by abdo last updated on 07/Aug/19
![1) ∫ (dx/(x(√(x+1))+(x+1)(√x))) =∫ (dx/( (√x)(√(x+1))((√x)+(√(x+1))))) =∫ (((√(x+1))−(√x))/( (√x)(√(x+1))))dx =∫(dx/( (√x))) −∫ (dx/( (√(x+1)))) =2(√x)−2(√(x+1)) +c 2)∫_1 ^(√3) (dx/(x(√(x+1))+(x+1)(√x))) =[2(√x)−2(√(x+1))]_1 ^(√3) =2^4 (√3)−2(√((√3)+1))−2+2(√2) .](https://www.tinkutara.com/question/Q65990.png)
$$\left.\mathrm{1}\right)\:\int\:\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}+\left({x}+\mathrm{1}\right)\sqrt{{x}}}\:=\int\:\:\frac{{dx}}{\:\sqrt{{x}}\sqrt{{x}+\mathrm{1}}\left(\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}\right)} \\ $$$$=\int\:\:\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}}}{\:\sqrt{{x}}\sqrt{{x}+\mathrm{1}}}{dx}\:=\int\frac{{dx}}{\:\sqrt{{x}}}\:−\int\:\frac{{dx}}{\:\sqrt{{x}+\mathrm{1}}}\:=\mathrm{2}\sqrt{{x}}−\mathrm{2}\sqrt{{x}+\mathrm{1}}\:+{c} \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}+\left({x}+\mathrm{1}\right)\sqrt{{x}}}\:=\left[\mathrm{2}\sqrt{{x}}−\mathrm{2}\sqrt{{x}+\mathrm{1}}\right]_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \\ $$$$=\mathrm{2}^{\mathrm{4}} \sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\sqrt{\mathrm{3}}+\mathrm{1}}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}\:. \\ $$
Answered by MJS last updated on 07/Aug/19
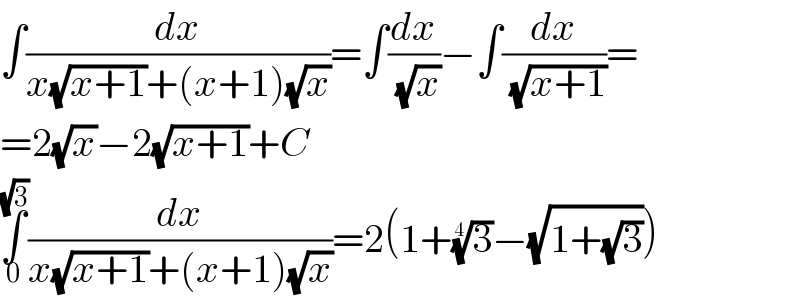
$$\int\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}+\left({x}+\mathrm{1}\right)\sqrt{{x}}}=\int\frac{{dx}}{\:\sqrt{{x}}}−\int\frac{{dx}}{\:\sqrt{{x}+\mathrm{1}}}= \\ $$$$=\mathrm{2}\sqrt{{x}}−\mathrm{2}\sqrt{{x}+\mathrm{1}}+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{3}}} {\int}}\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}+\left({x}+\mathrm{1}\right)\sqrt{{x}}}=\mathrm{2}\left(\mathrm{1}+\sqrt[{\mathrm{4}}]{\mathrm{3}}−\sqrt{\mathrm{1}+\sqrt{\mathrm{3}}}\right) \\ $$
