Question-46085

Question Number 46085 by peter frank last updated on 20/Oct/18

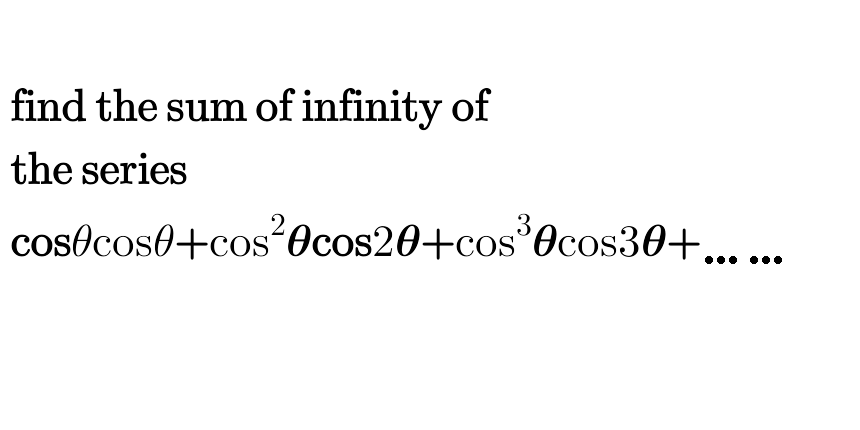
Commented by maxmathsup by imad last updated on 21/Oct/18

let S =Σ_(n=1) ^∞ cos^n θ cos(nθ) =Re( Σ_(n=1) ^∞ e^(inθ) cos^n θ) but Σ_(n=1) ^∞ e^(inθ) cos^n θ =Σ_(n=1) ^∞ e^(inθ) (((e^(iθ) +e^(−iθ) )/2))^n =Σ_(n=1) ^∞ (e^(inθ) /2^n ) (Σ_(k=0) ^n C_n ^k e^(ikθ) e^(−i(n−k)θ) ) =Σ_(n=1) ^∞ (1/2^n )(Σ_(k=0) ^n C_n ^k e^(2ikθ) ) =Σ_(n=1) ^∞ (1/2^n )Σ_(k=0) ^n C_n ^k (e^(2iθ) )^k =Σ_(n=1) ^∞ (1/2^n )(1+e^(2iθ) )^n =Σ_(n=1) ^∞ (((1+e^(2iθ) )/2))^n =(1/(1−((1+e^(2iθ) )/2))) −1 =(2/(1−e^(2iθ) )) −1 = ((2−1 +e^(2iθ) )/(1−e^(2iθ) )) = ((1+e^(2iθ) )/(1−e^(2iθ) )) =((1+cos(2θ)+i sin(2θ))/(1−cos(2θ)−isin(2θ))) =((2cos^2 (θ) +2i sinθ cosθ)/(2sin^2 θ−2isinθ cosθ)) =((cosθ e^(iθ) )/(−isinθ e^(iθ) )) = i cotanθ ⇒ S =0

$${let}\:{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{cos}^{{n}} \theta\:{cos}\left({n}\theta\right)\:={Re}\left(\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{e}^{{in}\theta} \:{cos}^{{n}} \theta\right)\:\:{but}\: \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:{e}^{{in}\theta} \:{cos}^{{n}} \theta\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{e}^{{in}\theta} \left(\frac{{e}^{{i}\theta} \:+{e}^{−{i}\theta} }{\mathrm{2}}\right)^{{n}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{e}^{{in}\theta} }{\mathrm{2}^{{n}} }\:\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:{e}^{{ik}\theta} \:{e}^{−{i}\left({n}−{k}\right)\theta} \right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:{e}^{\mathrm{2}{ik}\theta} \right)\:\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:\left({e}^{\mathrm{2}{i}\theta} \right)^{{k}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\mathrm{1}+{e}^{\mathrm{2}{i}\theta} \right)^{{n}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(\frac{\mathrm{1}+{e}^{\mathrm{2}{i}\theta} }{\mathrm{2}}\right)^{{n}} \:\:=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}+{e}^{\mathrm{2}{i}\theta} }{\mathrm{2}}}\:−\mathrm{1} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−{e}^{\mathrm{2}{i}\theta} }\:−\mathrm{1}\:=\:\frac{\mathrm{2}−\mathrm{1}\:+{e}^{\mathrm{2}{i}\theta} }{\mathrm{1}−{e}^{\mathrm{2}{i}\theta} }\:=\:\frac{\mathrm{1}+{e}^{\mathrm{2}{i}\theta} }{\mathrm{1}−{e}^{\mathrm{2}{i}\theta} }\:=\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)+{i}\:{sin}\left(\mathrm{2}\theta\right)}{\mathrm{1}−{cos}\left(\mathrm{2}\theta\right)−{isin}\left(\mathrm{2}\theta\right)} \\ $$$$=\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\theta\right)\:+\mathrm{2}{i}\:{sin}\theta\:{cos}\theta}{\mathrm{2}{sin}^{\mathrm{2}} \theta−\mathrm{2}{isin}\theta\:{cos}\theta}\:=\frac{{cos}\theta\:{e}^{{i}\theta} }{−{isin}\theta\:{e}^{{i}\theta} }\:=\:{i}\:{cotan}\theta\:\:\:\Rightarrow\:{S}\:=\mathrm{0} \\ $$$$ \\ $$

Commented by peter frank last updated on 21/Oct/18

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 21/Oct/18

p=cosθcosθ+cos^2 θcos2θ+cos^3 θcos3θ+... q=cosθsinθ+cos^2 θsin2θ+cos^3 θsin3θ+... now e^(iα) =cosα+isinα p+iq=cosθe^(iθ) +cos^2 θe^(i2θ) +cos^3 θe^(i3θ) +... p+iq=t+t^2 +t^3 +...∞ here i am editing... sum of terms upto infinity S_∞ =(t/(1−t))=((cosθe^(iθ) )/(1−cosθe^(iθ) )) =((cosθ(cosθ+isinθ))/(1−cosθ(cosθ+isinθ))) =((cosθ(cosθ+isnθ))/(1−cosθ(cosθ+isinθ))) =((cos^2 θ+isinθcosθ)/(1−cos^2 θ−isinθcosθ)) =((cosθ)/(sinθ))×((cosθ+isinθ)/(sinθ−icosθ)) =cotθ×(((cosθ+isinθ)(sinθ+icosθ))/((sinθ−icosθ)(sinθ+icosθ))) =cotθ×((cosθsinθ+icos^2 θ+isin^2 θ−sinθcosθ)/(sin^2 θ+cos^2 θ)) =cotθ×i so p+iq=0+icotθ so p=0 q=cotθ so required answer for the given series is zero

$${p}={cos}\theta{cos}\theta+{cos}^{\mathrm{2}} \theta{cos}\mathrm{2}\theta+{cos}^{\mathrm{3}} \theta{cos}\mathrm{3}\theta+… \\ $$$${q}={cos}\theta{sin}\theta+{cos}^{\mathrm{2}} \theta{sin}\mathrm{2}\theta+{cos}^{\mathrm{3}} \theta{sin}\mathrm{3}\theta+… \\ $$$${now}\:{e}^{{i}\alpha} ={cos}\alpha+{isin}\alpha \\ $$$${p}+{iq}={cos}\theta{e}^{{i}\theta} +{cos}^{\mathrm{2}} \theta{e}^{{i}\mathrm{2}\theta} +{cos}^{\mathrm{3}} \theta{e}^{{i}\mathrm{3}\theta} +… \\ $$$${p}+{iq}={t}+{t}^{\mathrm{2}} +{t}^{\mathrm{3}} +…\infty \\ $$$${here}\:{i}\:{am}\:{editing}… \\ $$$${sum}\:{of}\:{terms}\:{upto}\:{infinity} \\ $$$${S}_{\infty} =\frac{{t}}{\mathrm{1}−{t}}=\frac{{cos}\theta{e}^{{i}\theta} }{\mathrm{1}−{cos}\theta{e}^{{i}\theta} } \\ $$$$=\frac{{cos}\theta\left({cos}\theta+{isin}\theta\right)}{\mathrm{1}−{cos}\theta\left({cos}\theta+{isin}\theta\right)} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$=\frac{{cos}\theta\left({cos}\theta+{isn}\theta\right)}{\mathrm{1}−{cos}\theta\left({cos}\theta+{isin}\theta\right)} \\ $$$$=\frac{{cos}^{\mathrm{2}} \theta+{isin}\theta{cos}\theta}{\mathrm{1}−{cos}^{\mathrm{2}} \theta−{isin}\theta{cos}\theta} \\ $$$$=\frac{{cos}\theta}{{sin}\theta}×\frac{{cos}\theta+{isin}\theta}{{sin}\theta−{icos}\theta} \\ $$$$={cot}\theta×\frac{\left({cos}\theta+{isin}\theta\right)\left({sin}\theta+{icos}\theta\right)}{\left({sin}\theta−{icos}\theta\right)\left({sin}\theta+{icos}\theta\right)} \\ $$$$={cot}\theta×\frac{{cos}\theta{sin}\theta+{icos}^{\mathrm{2}} \theta+{isin}^{\mathrm{2}} \theta−{sin}\theta{cos}\theta}{{sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta} \\ $$$$={cot}\theta×{i} \\ $$$${so}\:{p}+{iq}=\mathrm{0}+{icot}\theta \\ $$$${so}\:{p}=\mathrm{0} \\ $$$${q}={cot}\theta \\ $$$$ \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{required}}\:\boldsymbol{{answer}}\:\boldsymbol{{for}}\:\boldsymbol{{the}}\:\boldsymbol{{given}}\:\boldsymbol{{series}}\:\boldsymbol{{is}}\:\boldsymbol{{zero}} \\ $$$$ \\ $$

Commented by peter frank last updated on 21/Oct/18