Question Number 46087 by Saorey last updated on 21/Oct/18
))dx thanks!!!](https://www.tinkutara.com/question/Q46087.png)
$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}!! \\ $$$$\mathrm{calculate}: \\ $$$$\mathrm{I}=\underset{\mathrm{2}} {\overset{\mathrm{1}+\mathrm{e}^{\mathrm{2}} } {\int}}\frac{\mathrm{12288ln}\left(\mathrm{x}−\mathrm{1}\right)}{\left[\mathrm{ln}^{\mathrm{12}} \left(\mathrm{x}−\mathrm{1}\right)+\mathrm{4096}\right]\left(\mathrm{x}−\mathrm{1}\right)}\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{thanks}!!! \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Oct/18
))dx t=ln(x−1) dt=(dx/(x−1)) ∫_0 ^2 ((12288t)/(t^(12) +4096))dt 6144∫_0 ^2 ((2t)/((t^2 )^6 +4096))dt k=t^(2 ) dk=2tdt 6144∫_0 ^4 (dk/(k^6 +4096)) 6144∫_0 ^4 (dk/(k^6 +4^6 )) ≈0 the curve (1/(x^6 +4^6 )) concide with x axis so area under the curve ∫_0 ^4 (dk/(k^6 +4^6 ))≈0](https://www.tinkutara.com/question/Q46094.png)
$$\int_{\mathrm{2}} ^{{e}^{\mathrm{2}} +\mathrm{1}} \frac{\mathrm{12288}{ln}\left({x}−\mathrm{1}\right)}{\left[{ln}^{\mathrm{12}} \left({x}−\mathrm{1}\right)+\mathrm{4096}\right]\left({x}−\mathrm{1}\right)}{dx} \\ $$$${t}={ln}\left({x}−\mathrm{1}\right)\:\:\:{dt}=\frac{{dx}}{{x}−\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{12288}{t}}{{t}^{\mathrm{12}} +\mathrm{4096}}{dt} \\ $$$$\mathrm{6144}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2}{t}}{\left({t}^{\mathrm{2}} \right)^{\mathrm{6}} +\mathrm{4096}}{dt}\:\:\:{k}={t}^{\mathrm{2}\:} \:{dk}=\mathrm{2}{tdt} \\ $$$$\mathrm{6144}\int_{\mathrm{0}} ^{\mathrm{4}} \frac{{dk}}{{k}^{\mathrm{6}} +\mathrm{4096}} \\ $$$$\mathrm{6144}\int_{\mathrm{0}} ^{\mathrm{4}} \frac{{dk}}{{k}^{\mathrm{6}} +\mathrm{4}^{\mathrm{6}} }\:\approx\mathrm{0} \\ $$$$ \\ $$$${the}\:{curve}\:\frac{\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{4}^{\mathrm{6}} }\:{concide}\:{with}\:{x}\:{axis} \\ $$$${so}\:{area}\:{under}\:{the}\:{curve}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \frac{{dk}}{{k}^{\mathrm{6}} +\mathrm{4}^{\mathrm{6}} }\approx\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Oct/18
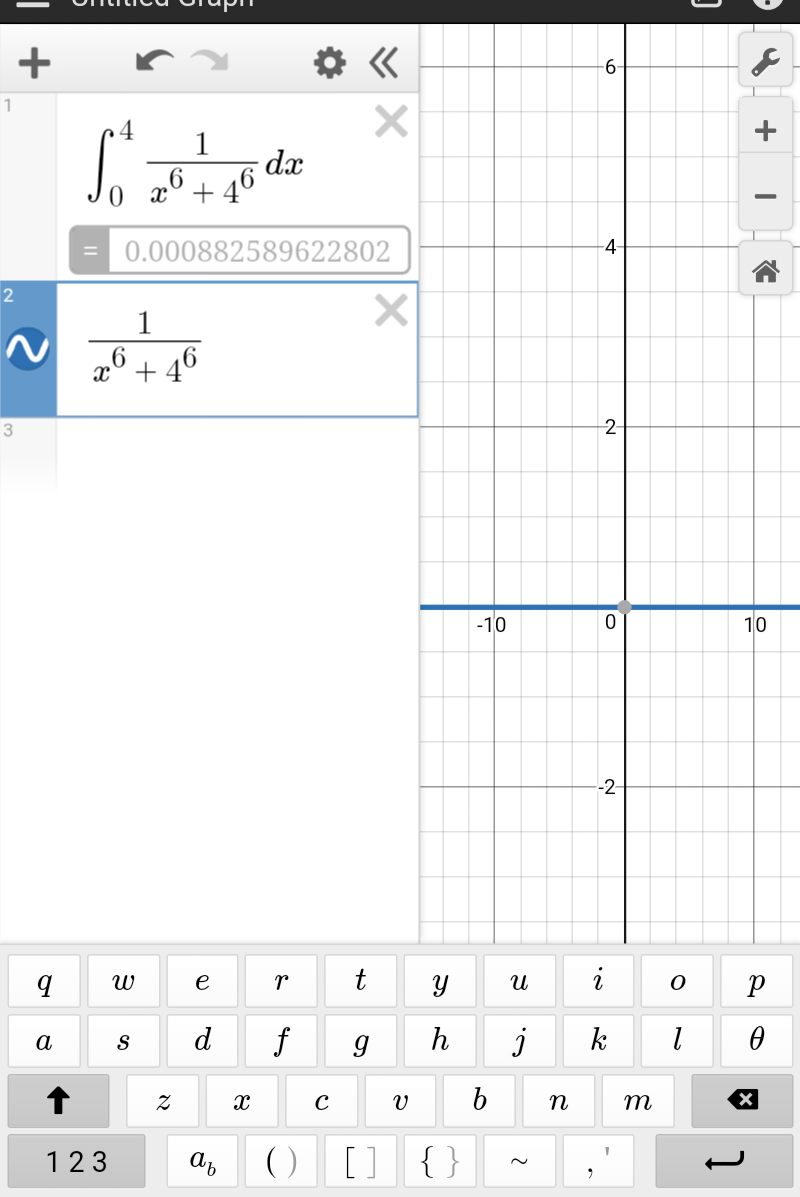
Commented by Saorey last updated on 21/Oct/18
thank you��
