Menu Close

Using-the-cosine-rule-c-2-a-2-b-2-2abcosC-prove-the-triangle-inequality-if-a-b-and-c-are-sides-of-a-triangle-ABC-then-a-b-c-and-explain-when-equality-holds-Further-prove-that-sin-sin-s

Tinku Tara 0 Comments
Pin




Question Number 112059 by Aina Samuel Temidayo last updated on 05/Sep/20
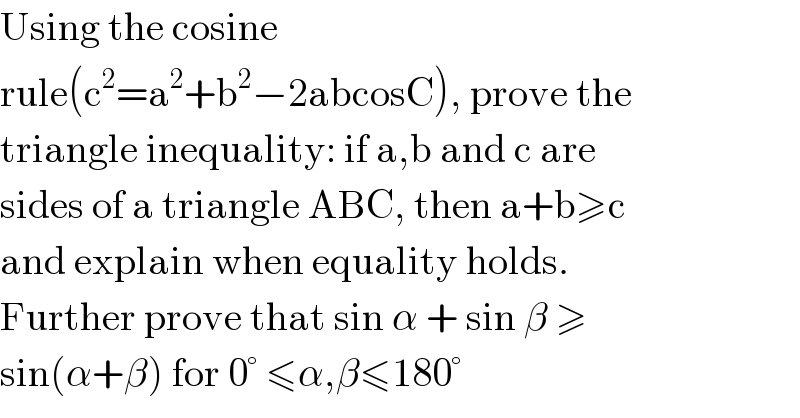
Using the cosine rule(c^2 =a^2 +b^2 −2abcosC), prove the triangle inequality: if a,b and c are sides of a triangle ABC, then a+b≥c and explain when equality holds. Further prove that sin α + sin β ≥ sin(α+β) for 0° ≤α,β≤180°
$$\mathrm{Using}\:\mathrm{the}\:\mathrm{cosine} \\ $$$$\mathrm{rule}\left(\mathrm{c}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2abcosC}\right),\:\mathrm{prove}\:\mathrm{the} \\ $$$$\mathrm{triangle}\:\mathrm{inequality}:\:\mathrm{if}\:\mathrm{a},\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{are} \\ $$$$\mathrm{sides}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{ABC},\:\mathrm{then}\:\mathrm{a}+\mathrm{b}\geqslant\mathrm{c} \\ $$$$\mathrm{and}\:\mathrm{explain}\:\mathrm{when}\:\mathrm{equality}\:\mathrm{holds}. \\ $$$$\mathrm{Further}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{sin}\:\alpha\:+\:\mathrm{sin}\:\beta\:\geqslant \\ $$$$\mathrm{sin}\left(\alpha+\beta\right)\:\mathrm{for}\:\mathrm{0}°\:\leqslant\alpha,\beta\leqslant\mathrm{180}° \\ $$
Answered by 1549442205PVT last updated on 06/Sep/20
i)From the cosine theorem we have c^2 =b^2 +a^2 −2abcosC ⇒a^2 +b^2 +2ab=c^2 +2abcosC+2ab ⇒(a+b)^2 =c^2 +2ab(1+cosC)(1) Since C is an angle of the triangle ,0<C<180° ⇒cosC>−1⇒1+cosC>0.Hence, c^2 +2ab(1+cosC)>c^2 (2) From (1)(2) we infer (a+b)^2 >c^2 ⇒a+b>c ii)We have sin(α+β)=sinαcosβ+cosαsinβ Since 0<α,β≤180°,sinα,sinβ>0.Also, cosα,cosβ≤1.Hence sinαcosβ≤sinα(3) sinβcosα≤sinβ (4) From (3)(4)we get sin(α+β)= sinαcosβ+cosαsinβ≤sinα+sinβ(q.e.d) iii)Prove sinα+sinβ≥2sin((α+β)/2) By the convert formula for the sum of two sine we have sinα+sinβ=2sin((α+β)/2)cos((α−β)/2) (5) Since 0<α<180 ,0<((α+β)/2)<90° ⇒sin((α+β)/2)>0 .On the other hands, cos((α−β)/2)≤1.Hence,2sin((α+β)/2)cos((α+β)/2) ≤2sin((α+β)/2) (6).From(5)(6)we get sinα+sinβ≥2sin((α+β)/2) (q.e.d)
$$\left.\mathrm{i}\right)\mathrm{From}\:\mathrm{the}\:\mathrm{cosine}\:\mathrm{theorem}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{c}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{2abcosC} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2ab}=\mathrm{c}^{\mathrm{2}} +\mathrm{2abcosC}+\mathrm{2ab} \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} =\mathrm{c}^{\mathrm{2}} +\mathrm{2ab}\left(\mathrm{1}+\mathrm{cosC}\right)\left(\mathrm{1}\right) \\ $$$$\mathrm{Since}\:\mathrm{C}\:\mathrm{is}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\:,\mathrm{0}<\mathrm{C}<\mathrm{180}° \\ $$$$\Rightarrow\mathrm{cosC}>−\mathrm{1}\Rightarrow\mathrm{1}+\mathrm{cosC}>\mathrm{0}.\mathrm{Hence}, \\ $$$$\mathrm{c}^{\mathrm{2}} +\mathrm{2ab}\left(\mathrm{1}+\mathrm{cosC}\right)>\boldsymbol{\mathrm{c}}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{infer}\: \\ $$$$\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} >\mathrm{c}^{\mathrm{2}} \Rightarrow\mathrm{a}+\mathrm{b}>\mathrm{c} \\ $$$$\left.\mathrm{ii}\right)\mathrm{We}\:\mathrm{have}\:\mathrm{sin}\left(\alpha+\beta\right)=\mathrm{sin}\alpha\mathrm{cos}\beta+\mathrm{cos}\alpha\mathrm{sin}\beta \\ $$$$\mathrm{Since}\:\mathrm{0}<\alpha,\beta\leqslant\mathrm{180}°,\mathrm{sin}\alpha,\mathrm{sin}\beta>\mathrm{0}.\mathrm{Also}, \\ $$$$\mathrm{cos}\alpha,\mathrm{cos}\beta\leqslant\mathrm{1}.\mathrm{Hence} \\ $$$$\mathrm{sin}\alpha\mathrm{cos}\beta\leqslant\mathrm{sin}\alpha\left(\mathrm{3}\right) \\ $$$$\mathrm{sin}\beta\mathrm{cos}\alpha\leqslant\mathrm{sin}\beta\:\left(\mathrm{4}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{3}\right)\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{sin}\left(\alpha+\beta\right)= \\ $$$$\mathrm{sin}\alpha\mathrm{cos}\beta+\mathrm{cos}\alpha\mathrm{sin}\beta\leqslant\mathrm{sin}\alpha+\mathrm{sin}\beta\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$$$\left.\mathrm{iii}\right)\mathrm{Prove}\:\mathrm{sin}\alpha+\mathrm{sin}\beta\geqslant\mathrm{2sin}\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\mathrm{By}\:\mathrm{the}\:\mathrm{convert}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\mathrm{of}\:\mathrm{two}\:\mathrm{sine}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{sin}\alpha+\mathrm{sin}\beta=\mathrm{2sin}\frac{\alpha+\beta}{\mathrm{2}}\mathrm{cos}\frac{\alpha−\beta}{\mathrm{2}}\:\left(\mathrm{5}\right) \\ $$$$\mathrm{Since}\:\mathrm{0}<\alpha<\mathrm{180}\:,\mathrm{0}<\frac{\alpha+\beta}{\mathrm{2}}<\mathrm{90}° \\ $$$$\Rightarrow\mathrm{sin}\frac{\alpha+\beta}{\mathrm{2}}>\mathrm{0}\:.\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hands}, \\ $$$$\mathrm{cos}\frac{\alpha−\beta}{\mathrm{2}}\leqslant\mathrm{1}.\mathrm{Hence},\mathrm{2sin}\frac{\alpha+\beta}{\mathrm{2}}\mathrm{cos}\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\leqslant\mathrm{2sin}\frac{\alpha+\beta}{\mathrm{2}}\:\left(\mathrm{6}\right).\mathrm{From}\left(\mathrm{5}\right)\left(\mathrm{6}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{sin}\alpha+\mathrm{sin}\beta\geqslant\mathrm{2sin}\frac{\alpha+\beta}{\mathrm{2}}\:\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$
Commented by Aina Samuel Temidayo last updated on 06/Sep/20
From (1)(2) why do we infer (a+b)^2 >c^2 . I don′t understand please.
$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right) \\ $$$$\mathrm{why}\:\mathrm{do}\:\mathrm{we}\:\mathrm{infer}\:\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} >\mathrm{c}^{\mathrm{2}} .\:\mathrm{I}\:\mathrm{don}'\mathrm{t} \\ $$$$\mathrm{understand}\:\mathrm{please}. \\ $$
Commented by Aina Samuel Temidayo last updated on 06/Sep/20
For (ii), please how did sin α + sin β ≥ sin(α+β) change into sin α + sin β ≥2sin((α+β)/2)
$$\mathrm{For}\:\left(\mathrm{ii}\right),\:\mathrm{please}\:\mathrm{how}\:\mathrm{did}\:\mathrm{sin}\:\alpha\:+\:\mathrm{sin}\:\beta\:\geqslant \\ $$$$\mathrm{sin}\left(\alpha+\beta\right)\:\mathrm{change}\:\mathrm{into}\:\mathrm{sin}\:\alpha\:+\:\mathrm{sin}\:\beta \\ $$$$\geqslant\mathrm{2sin}\frac{\alpha+\beta}{\mathrm{2}} \\ $$
Commented by 1549442205PVT last updated on 06/Sep/20
I wrote a mistake and corrected
$$\mathrm{I}\:\mathrm{wrote}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{and}\:\mathrm{corrected} \\ $$
Commented by Aina Samuel Temidayo last updated on 06/Sep/20
I don′t get. What′s the mistake?
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}.\:\mathrm{What}'\mathrm{s}\:\mathrm{the}\:\mathrm{mistake}? \\ $$
Commented by Aina Samuel Temidayo last updated on 06/Sep/20
Oh. Thanks. But do I need (iii) ?
$$\mathrm{Oh}.\:\mathrm{Thanks}.\:\mathrm{But}\:\mathrm{do}\:\mathrm{I}\:\mathrm{need}\:\left(\mathrm{iii}\right)\:? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *