Question Number 177932 by Spillover last updated on 11/Oct/22
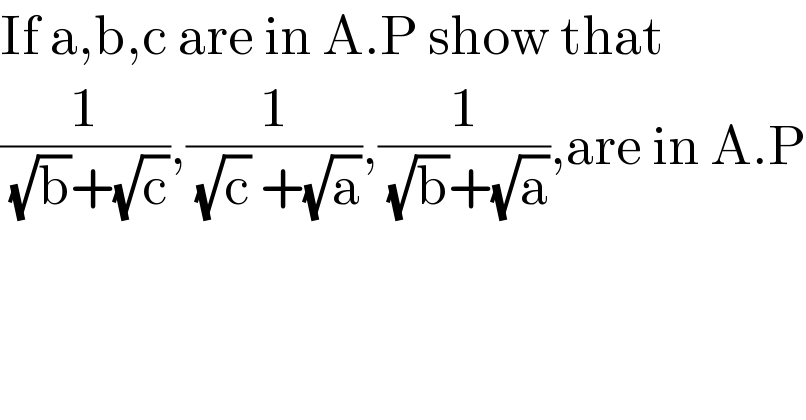
$$\mathrm{If}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{are}\:\mathrm{in}\:\mathrm{A}.\mathrm{P}\:\mathrm{show}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{b}}+\sqrt{\mathrm{c}}},\frac{\mathrm{1}}{\:\sqrt{\mathrm{c}}\:+\sqrt{\mathrm{a}}},\frac{\mathrm{1}}{\:\sqrt{\mathrm{b}}+\sqrt{\mathrm{a}}},\mathrm{are}\:\mathrm{in}\:\mathrm{A}.\mathrm{P} \\ $$
Answered by Ar Brandon last updated on 11/Oct/22
![a, b, c in AP ⇒b−a=c−b=d (common diff) If u_1 =(1/( (√b)+(√c))), u_2 =(1/( (√c)+(√b))), u_3 =(1/( (√b)+(√a))) are in AP then u_2 is the arithmetic mean of u_1 and u_3 ⇒ u_1 +u_3 =2u_2 (1/( (√b)+(√c))), (1/( (√c)+(√a))), (1/( (√b)+(√a))) ⇔ (((√c)−(√b))/(c−b)), (((√c)−(√a))/(c−a)), (((√b)−(√a))/(b−a)) ⇔(((√c)−(√b))/d), (((√c)−(√a))/(2d)), (((√b)−(√a))/d) [c−a=(c−b)+(b−a)=2d] Now u_1 =(((√c)−(√b))/d), u_2 =(((√c)−(√a))/(2d)), u_3 =(((√b)−(√a))/d) u_1 +u_3 =(((√c)−(√b))/d)+(((√b)−(√a))/d)=(((√c)−(√a))/d)=2u_2](https://www.tinkutara.com/question/Q177936.png)
$${a},\:{b},\:{c}\:\mathrm{in}\:{AP}\:\Rightarrow{b}−{a}={c}−{b}={d}\:\left(\mathrm{common}\:\mathrm{diff}\right) \\ $$$$\mathrm{If}\:{u}_{\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{{b}}+\sqrt{{c}}},\:{u}_{\mathrm{2}} =\frac{\mathrm{1}}{\:\sqrt{{c}}+\sqrt{{b}}},\:{u}_{\mathrm{3}} =\frac{\mathrm{1}}{\:\sqrt{{b}}+\sqrt{{a}}}\:\mathrm{are}\:\mathrm{in}\:\mathrm{AP} \\ $$$$\mathrm{then}\:{u}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{arithmetic}\:\mathrm{mean}\:\mathrm{of}\:{u}_{\mathrm{1}} \:\mathrm{and}\:{u}_{\mathrm{3}} \\ $$$$\Rightarrow\:{u}_{\mathrm{1}} +{u}_{\mathrm{3}} =\mathrm{2}{u}_{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{b}}+\sqrt{{c}}},\:\frac{\mathrm{1}}{\:\sqrt{{c}}+\sqrt{{a}}},\:\frac{\mathrm{1}}{\:\sqrt{{b}}+\sqrt{{a}}}\:\Leftrightarrow\:\frac{\sqrt{{c}}−\sqrt{{b}}}{{c}−{b}},\:\frac{\sqrt{{c}}−\sqrt{{a}}}{{c}−{a}},\:\frac{\sqrt{{b}}−\sqrt{{a}}}{{b}−{a}} \\ $$$$\Leftrightarrow\frac{\sqrt{{c}}−\sqrt{{b}}}{{d}},\:\frac{\sqrt{{c}}−\sqrt{{a}}}{\mathrm{2}{d}},\:\frac{\sqrt{{b}}−\sqrt{{a}}}{{d}}\:\:\left[{c}−{a}=\left({c}−{b}\right)+\left({b}−{a}\right)=\mathrm{2}{d}\right] \\ $$$$\mathrm{Now}\:{u}_{\mathrm{1}} =\frac{\sqrt{{c}}−\sqrt{{b}}}{{d}},\:{u}_{\mathrm{2}} =\frac{\sqrt{{c}}−\sqrt{{a}}}{\mathrm{2}{d}},\:{u}_{\mathrm{3}} =\frac{\sqrt{{b}}−\sqrt{{a}}}{{d}} \\ $$$${u}_{\mathrm{1}} +{u}_{\mathrm{3}} =\frac{\sqrt{{c}}−\sqrt{{b}}}{{d}}+\frac{\sqrt{{b}}−\sqrt{{a}}}{{d}}=\frac{\sqrt{{c}}−\sqrt{{a}}}{{d}}=\mathrm{2}{u}_{\mathrm{2}} \\ $$
