Question Number 177964 by mathlove last updated on 11/Oct/22
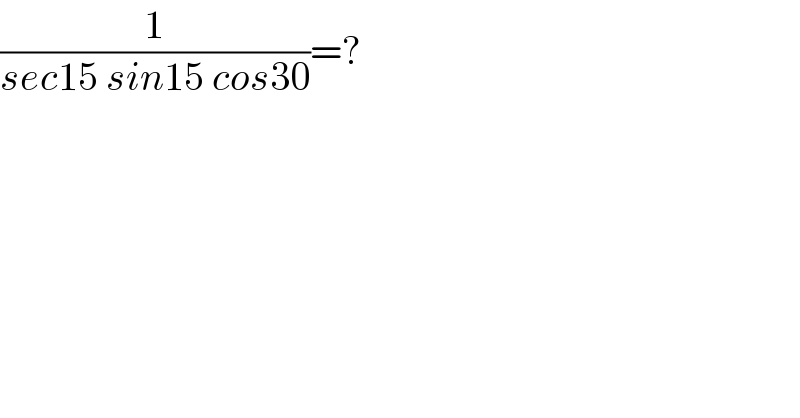
$$\frac{\mathrm{1}}{{sec}\mathrm{15}\:{sin}\mathrm{15}\:{cos}\mathrm{30}}=? \\ $$
Commented by cortano1 last updated on 11/Oct/22
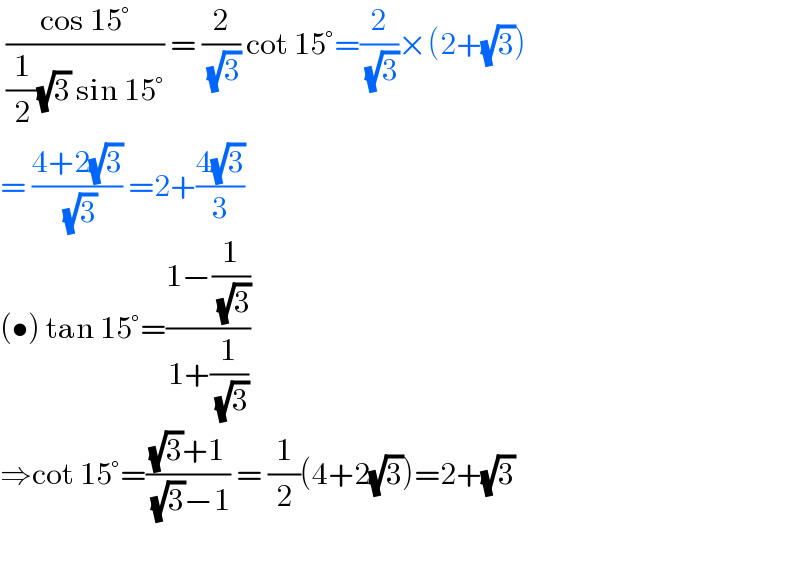
$$\:\frac{\mathrm{cos}\:\mathrm{15}°}{\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{15}°}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{cot}\:\mathrm{15}°=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}×\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$=\:\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}}\:=\mathrm{2}+\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\left(\bullet\right)\:\mathrm{tan}\:\mathrm{15}°=\frac{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \\ $$$$\Rightarrow\mathrm{cot}\:\mathrm{15}°=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}−\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 11/Oct/22

$$\frac{\mathrm{1}}{\mathrm{sec15}°\mathrm{sin15}°\mathrm{cos30}°}=\frac{\mathrm{cos15}°}{\mathrm{sin15}°}×\frac{\mathrm{1}}{\mathrm{cos30}°}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\mathrm{tan15}°} \\ $$$$\mathrm{cos2}{x}=\mathrm{2cos}^{\mathrm{2}} {x}−\mathrm{1}=\frac{\mathrm{2}}{\mathrm{sec}^{\mathrm{2}} {x}}−\mathrm{1}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos30}°=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{15}°}−\mathrm{1}\:,\:{x}=\mathrm{15}° \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{1}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{15}°}\:\Rightarrow\frac{\sqrt{\mathrm{3}}+\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{15}°} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{15}°=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}+\mathrm{2}}=\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\: \\ $$$$\Rightarrow\mathrm{tan15}°=\sqrt{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}}=\sqrt{\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{4}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{4}}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sec15}°\mathrm{sin15}°\mathrm{cos30}°}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{4}}−\sqrt{\mathrm{3}}\right)}=\frac{\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{3}}} \\ $$
Commented by mathlove last updated on 12/Oct/22

$${thanks} \\ $$
Answered by Rasheed.Sindhi last updated on 12/Oct/22

$$\frac{\mathrm{1}}{\mathrm{sec15sin15cos30}\:\:\:}=? \\ $$$$=\frac{\mathrm{1}}{\mathrm{sec15sin15}\underline{\underset{\blacktrinagledown} {\mathrm{sin60}}}\:\:\:} \\ $$$$\:\:\mathrm{sin60}=\mathrm{2sin30cos30}=\mathrm{2}\left(\mathrm{2sin15cos15}\right)\mathrm{cos30} \\ $$$$\:\:\:\:\:=\mathrm{4sin15cos15cos30}\: \\ $$$$=\frac{\mathrm{1}}{\cancel{\mathrm{sec15}sin15}\centerdot\mathrm{4sin15}\cancel{\mathrm{cos15}cos30}\:\:\:} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\underline{\underset{\blacktrinagledown} {\mathrm{sin}^{\mathrm{2}} \mathrm{15}}cos30}\:\:\:} \\ $$$$\:\:\mathrm{sin}^{\mathrm{2}} \alpha=\frac{\mathrm{1}−\mathrm{cos2}\alpha\:}{\mathrm{2}}\Rightarrow\mathrm{sin}^{\mathrm{2}} \mathrm{15}=\frac{\mathrm{1}−\mathrm{cos30}\:}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left(\frac{\mathrm{1}−\mathrm{cos30}\:}{\mathrm{2}}\right)\mathrm{cos30}\:} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2cos30}\left(\mathrm{1}−\mathrm{cos30}\right)}=\frac{\mathrm{1}}{\cancel{\mathrm{2}}\left(\frac{\sqrt{\mathrm{3}}\:}{\cancel{\mathrm{2}}}\right)\left(\mathrm{1}−\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3}}\:−\mathrm{3}}\centerdot\frac{\mathrm{2}\sqrt{\mathrm{3}}\:+\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{3}}\:+\mathrm{3}}=\frac{\mathrm{4}\sqrt{\mathrm{3}}\:+\mathrm{6}}{\mathrm{3}} \\ $$$$\mathcal{F}{ormulas}\:\:\mathcal{U}{sed}:\:\:\bullet\mathrm{sin2}\alpha=\mathrm{2sin}\alpha\mathrm{cos}\alpha\:\:\: \\ $$$$\begin{array}{|c|}{\:\begin{array}{|c|}{\underset{\:\underset{\:\:\:\:\:\:\:\:\:\bullet\mathrm{sin2}\alpha=\mathrm{2sin}\alpha\mathrm{cos}\alpha} {\:}} {\bullet\mathrm{sin}^{\mathrm{2}} \alpha=\frac{\mathrm{1}−\mathrm{cos2}\alpha\:}{\mathrm{2}}}}\\\hline\end{array}_{\:} ^{\:} }\\\hline\end{array} \\ $$
Commented by Tawa11 last updated on 11/Oct/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Commented by mathlove last updated on 12/Oct/22

$${thanks}\:{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 12/Oct/22
![(1/(sec15sin15cos30 ))=? =(1/(sec15sec15cos15 sin15cos30 )) [∵sec15cos15=1] =(1/(sec^2 15∙(1/2)sin30 cos30 )) [∵ cosα sinα=(1/2)sin2α] =(1/((2/(1+cos30 ))∙(1/2)sin30 cos30 )) [∵ sec^2 α=(2/(1+cos2α ))] =(1/((1/(1+cos30 ))∙(1/2)sin60 )) =2(1+cos30)∙(1/(sin60)) ={2+2((((√3) )/2))}.(2/( (√3)))=((4+2(√3))/( (√3)))∙(((√3) )/( (√3)))=((6+4(√3) )/3)](https://www.tinkutara.com/question/Q178050.png)
$$\frac{\mathrm{1}}{\mathrm{sec15sin15cos30}\:\:\:}=? \\ $$$$=\frac{\mathrm{1}}{\mathrm{sec15sec15}\underline{\mathrm{cos15}\:\mathrm{sin15}cos30}\:\:\:}\:\left[\because\mathrm{sec15cos15}=\mathrm{1}\right]\:\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{2}} \mathrm{15}\centerdot\underline{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin30}}\:\mathrm{cos30}\:\:\:}\:\left[\because\:\mathrm{cos}\alpha\:\mathrm{sin}\alpha=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2}\alpha\right]\: \\ $$$$=\frac{\mathrm{1}}{\frac{\cancel{\mathrm{2}}}{\mathrm{1}+\mathrm{cos30}\:}\centerdot\frac{\mathrm{1}}{\cancel{\mathrm{2}}}\mathrm{sin30}\:\mathrm{cos30}\:\:\:}\:\left[\because\:\mathrm{sec}^{\mathrm{2}} \alpha=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{cos2}\alpha\:}\right]\: \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos30}\:}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin60}\:\:\:} \\ $$$$=\mathrm{2}\left(\mathrm{1}+\mathrm{cos30}\right)\centerdot\frac{\mathrm{1}}{\mathrm{sin60}}\: \\ $$$$=\left\{\mathrm{2}+\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)\right\}.\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}}\centerdot\frac{\sqrt{\mathrm{3}}\:}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{6}+\mathrm{4}\sqrt{\mathrm{3}}\:}{\mathrm{3}} \\ $$
