Question Number 47064 by maxmathsup by imad last updated on 04/Nov/18
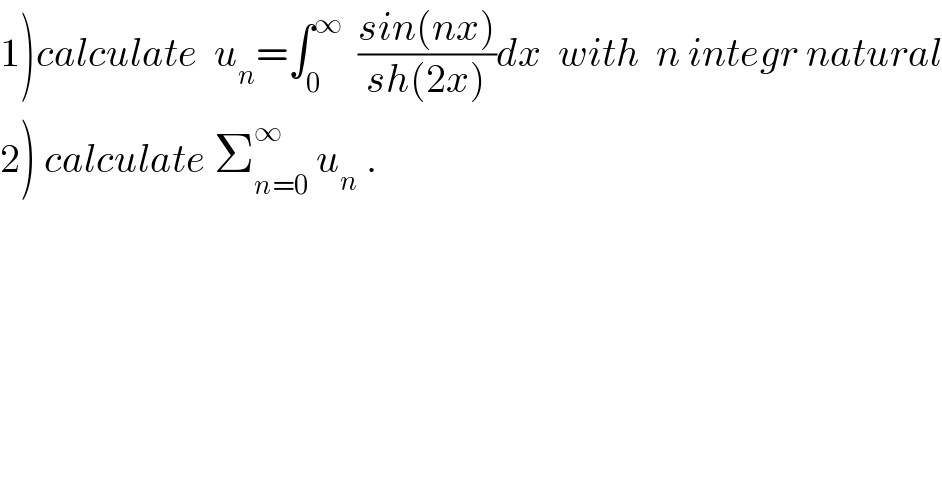
$$\left.\mathrm{1}\right){calculate}\:\:{u}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({nx}\right)}{{sh}\left(\mathrm{2}{x}\right)}{dx}\:\:{with}\:\:{n}\:{integr}\:{natural} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}_{{n}} \:. \\ $$
Commented by maxmathsup by imad last updated on 07/Nov/18
![1) we have u_n =∫_0 ^∞ ((2sin(nx))/(e^(2x) −e^(−2x) ))dx =2∫_0 ^∞ ((e^(−2x) sin(nx))/(1−e^(−4x) ))dx =2 ∫_0 ^∞ e^(−2x) sin(nx)(Σ_(p=0) ^∞ e^(−4px) )ex =2 Σ_(p=0) ^∞ ∫_0 ^∞ e^(−(2+4p)x) sin(nx)dx =_((2+4p)x=u) 2 Σ_(p=0) ^∞ ∫_0 ^∞ e^(−u) sin(n(u/(2+4p)))(du/(2+4p)) =Σ_(p=0) ^∞ (1/(2p+1)) ∫_0 ^∞ e^(−u) sin(((nu)/(4p+2)))du let determine I_λ =∫_0 ^∞ e^(−u) sin(λu)du (λ>0) I_λ =Im(∫_0 ^∞ e^(−u+iλu) du)=Im(∫_0 ^∞ e^((−1+iλ)u) du) but ∫_0 ^∞ e^((−1+iλ)u) du =[(1/(−1+iλ)) e^((−1+iλ)u) ]_0 ^(+∞) =((−1)/(−1+iλ)) =(1/(1−iλ)) =((1+iλ)/(1+λ^2 )) ⇒ I_λ =(λ/(1+λ^2 )) ⇒u_n =Σ_(p=0) ^∞ (1/(2p+1)) ((n/((4p+2)(1+((n/(4p+2)))^2 )))) =Σ_(p=0) ^∞ (n/((2p+1)(4p+2 +(n^2 /(4p+2))))) =Σ_(p=0) ^∞ ((n(4p+2))/((2p+1)((4p+2)^2 +n^2 ))) =Σ_(p=0) ^∞ ((2n)/((4p+2)^2 +n^2 )) u_n can be calculated by fourier serie ....be continued....](https://www.tinkutara.com/question/Q47297.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{u}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{sin}\left({nx}\right)}{{e}^{\mathrm{2}{x}} −{e}^{−\mathrm{2}{x}} }{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\mathrm{2}{x}} {sin}\left({nx}\right)}{\mathrm{1}−{e}^{−\mathrm{4}{x}} }{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{x}} {sin}\left({nx}\right)\left(\sum_{{p}=\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{4}{px}} \right){ex} \\ $$$$=\mathrm{2}\:\sum_{{p}=\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \:{e}^{−\left(\mathrm{2}+\mathrm{4}{p}\right){x}} {sin}\left({nx}\right){dx} \\ $$$$=_{\left(\mathrm{2}+\mathrm{4}{p}\right){x}={u}} \:\:\mathrm{2}\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}} \:{sin}\left({n}\frac{{u}}{\mathrm{2}+\mathrm{4}{p}}\right)\frac{{du}}{\mathrm{2}+\mathrm{4}{p}} \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}{p}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{u}} {sin}\left(\frac{{nu}}{\mathrm{4}{p}+\mathrm{2}}\right){du}\:\:{let}\:{determine}\:{I}_{\lambda} =\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}} \:{sin}\left(\lambda{u}\right){du}\:\left(\lambda>\mathrm{0}\right) \\ $$$${I}_{\lambda} ={Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}+{i}\lambda{u}} {du}\right)={Im}\left(\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−\mathrm{1}+{i}\lambda\right){u}} {du}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−\mathrm{1}+{i}\lambda\right){u}} {du}\:=\left[\frac{\mathrm{1}}{−\mathrm{1}+{i}\lambda}\:{e}^{\left(−\mathrm{1}+{i}\lambda\right){u}} \right]_{\mathrm{0}} ^{+\infty} \:=\frac{−\mathrm{1}}{−\mathrm{1}+{i}\lambda}\:=\frac{\mathrm{1}}{\mathrm{1}−{i}\lambda}\:=\frac{\mathrm{1}+{i}\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}_{\lambda} =\frac{\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }\:\Rightarrow{u}_{{n}} =\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}{p}+\mathrm{1}}\:\left(\frac{{n}}{\left(\mathrm{4}{p}+\mathrm{2}\right)\left(\mathrm{1}+\left(\frac{{n}}{\mathrm{4}{p}+\mathrm{2}}\right)^{\mathrm{2}} \right)}\right) \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\frac{{n}}{\left(\mathrm{2}{p}+\mathrm{1}\right)\left(\mathrm{4}{p}+\mathrm{2}\:+\frac{{n}^{\mathrm{2}} }{\mathrm{4}{p}+\mathrm{2}}\right)}\:=\sum_{{p}=\mathrm{0}} ^{\infty} \frac{{n}\left(\mathrm{4}{p}+\mathrm{2}\right)}{\left(\mathrm{2}{p}+\mathrm{1}\right)\left(\left(\mathrm{4}{p}+\mathrm{2}\right)^{\mathrm{2}} \:+{n}^{\mathrm{2}} \right)}\:=\sum_{{p}=\mathrm{0}} ^{\infty} \frac{\mathrm{2}{n}}{\left(\mathrm{4}{p}+\mathrm{2}\right)^{\mathrm{2}} \:+{n}^{\mathrm{2}} } \\ $$$${u}_{{n}} \:{can}\:{be}\:{calculated}\:{by}\:{fourier}\:{serie}\:….{be}\:{continued}…. \\ $$$$ \\ $$
