Question Number 47454 by peter frank last updated on 10/Nov/18
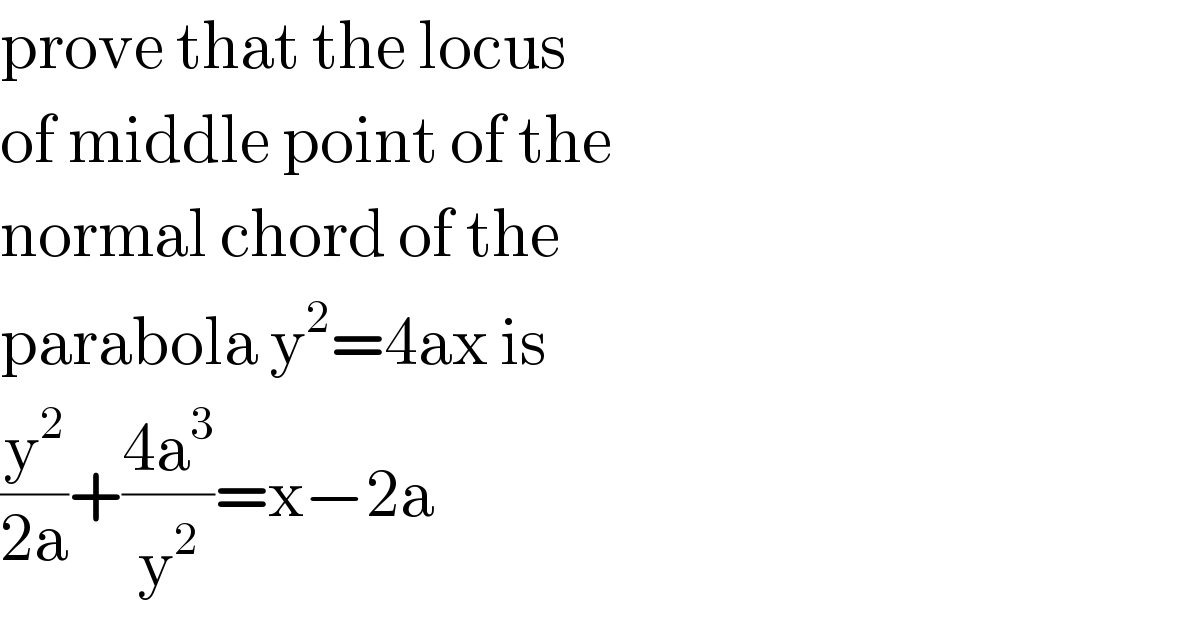
$$\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{locus} \\ $$$$\mathrm{of}\:\mathrm{middle}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{normal}\:\mathrm{chord}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{parabola}\:\mathrm{y}^{\mathrm{2}} =\mathrm{4ax}\:\mathrm{is} \\ $$$$\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{2a}}+\frac{\mathrm{4a}^{\mathrm{3}} }{\mathrm{y}^{\mathrm{2}} }=\mathrm{x}−\mathrm{2a} \\ $$
Answered by ajfour last updated on 10/Nov/18
![M(h,k) y=2at ; x=at^2 M is midpoint of chord, so ⇒ k−2at_1 = −t_1 (h−at_1 ^2 ) ....(i) 2a(t_2 +t_1 )=2k ...(ii) a(t_2 ^2 +t_1 ^2 )=2h ...(iii) ⇒ ((2a(t_2 −t_1 ))/(a(t_2 ^2 −t_1 ^2 )))= −t_1 ⇒ t_1 (t_1 +t_2 )= −2 ...(iv) using (ii) in (iv) t_1 ((k/a))=−2 ⇒ t_1 = ((−2a)/k) using this in (i) k−2a(((−2a)/k))= (((2a)/k))[h−a(((4a^2 )/k^2 ))] Now (h,k)→(x,y) (y+((4a^2 )/y))((y/(2a)))= x−((4a^3 )/y^2 ) ⇒ (y^2 /(2a))+2a = x−((4a^3 )/y^2 ) or (y^2 /(2a)) + ((4a^3 )/y^2 ) = x−2a .](https://www.tinkutara.com/question/Q47458.png)
$${M}\left({h},{k}\right) \\ $$$${y}=\mathrm{2}{at}\:\:;\:{x}={at}^{\mathrm{2}} \\ $$$${M}\:{is}\:{midpoint}\:{of}\:{chord},\:{so} \\ $$$$\Rightarrow\:\:{k}−\mathrm{2}{at}_{\mathrm{1}} =\:−{t}_{\mathrm{1}} \left({h}−{at}_{\mathrm{1}} ^{\mathrm{2}} \right)\:\:\:\:\:\:\:\:….\left({i}\right) \\ $$$$\:\:\:\mathrm{2}{a}\left({t}_{\mathrm{2}} +{t}_{\mathrm{1}} \right)=\mathrm{2}{k}\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\:\:\:\:{a}\left({t}_{\mathrm{2}} ^{\mathrm{2}} +{t}_{\mathrm{1}} ^{\mathrm{2}} \right)=\mathrm{2}{h}\:\:\:\:\:\:\:…\left({iii}\right) \\ $$$$\Rightarrow\:\frac{\mathrm{2}{a}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)}{{a}\left({t}_{\mathrm{2}} ^{\mathrm{2}} −{t}_{\mathrm{1}} ^{\mathrm{2}} \right)}=\:−{t}_{\mathrm{1}} \\ $$$$\Rightarrow\:\:\:{t}_{\mathrm{1}} \left({t}_{\mathrm{1}} +{t}_{\mathrm{2}} \right)=\:−\mathrm{2}\:\:\:\:\:\:…\left({iv}\right) \\ $$$${using}\:\left({ii}\right)\:{in}\:\left({iv}\right) \\ $$$$\:\:\:\:\:{t}_{\mathrm{1}} \left(\frac{{k}}{{a}}\right)=−\mathrm{2} \\ $$$$\Rightarrow\:\:\:{t}_{\mathrm{1}} \:=\:\frac{−\mathrm{2}{a}}{{k}} \\ $$$${using}\:{this}\:{in}\:\left({i}\right) \\ $$$$\:\:{k}−\mathrm{2}{a}\left(\frac{−\mathrm{2}{a}}{{k}}\right)=\:\left(\frac{\mathrm{2}{a}}{{k}}\right)\left[{h}−{a}\left(\frac{\mathrm{4}{a}^{\mathrm{2}} }{{k}^{\mathrm{2}} }\right)\right] \\ $$$${Now}\:\left({h},{k}\right)\rightarrow\left({x},{y}\right) \\ $$$$\left({y}+\frac{\mathrm{4}{a}^{\mathrm{2}} }{{y}}\right)\left(\frac{{y}}{\mathrm{2}{a}}\right)=\:{x}−\frac{\mathrm{4}{a}^{\mathrm{3}} }{{y}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\frac{{y}^{\mathrm{2}} }{\mathrm{2}{a}}+\mathrm{2}{a}\:=\:{x}−\frac{\mathrm{4}{a}^{\mathrm{3}} }{{y}^{\mathrm{2}} } \\ $$$${or}\:\:\:\:\:\frac{{y}^{\mathrm{2}} }{\mathrm{2}{a}}\:+\:\frac{\mathrm{4}{a}^{\mathrm{3}} }{{y}^{\mathrm{2}} }\:=\:{x}−\mathrm{2}{a}\:. \\ $$
