Question Number 113221 by frc2crc last updated on 11/Sep/20
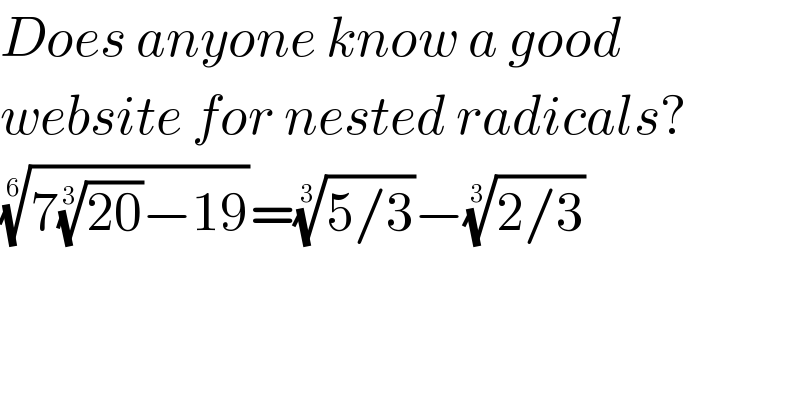
$${Does}\:{anyone}\:{know}\:{a}\:{good} \\ $$$${website}\:{for}\:{nested}\:{radicals}? \\ $$$$\sqrt[{\mathrm{6}}]{\mathrm{7}\sqrt[{\mathrm{3}}]{\mathrm{20}}−\mathrm{19}}=\sqrt[{\mathrm{3}}]{\mathrm{5}/\mathrm{3}}−\sqrt[{\mathrm{3}}]{\mathrm{2}/\mathrm{3}} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Sep/20
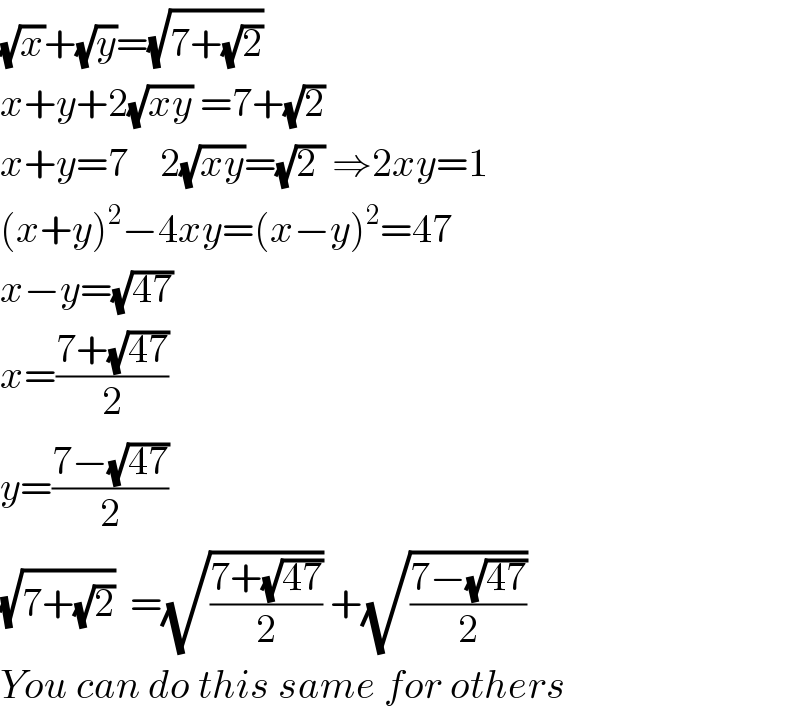
$$\sqrt{{x}}+\sqrt{{y}}=\sqrt{\mathrm{7}+\sqrt{\mathrm{2}}} \\ $$$${x}+{y}+\mathrm{2}\sqrt{{xy}}\:=\mathrm{7}+\sqrt{\mathrm{2}} \\ $$$${x}+{y}=\mathrm{7}\:\:\:\:\mathrm{2}\sqrt{{xy}}=\sqrt{\mathrm{2}\:}\:\Rightarrow\mathrm{2}{xy}=\mathrm{1} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy}=\left({x}−{y}\right)^{\mathrm{2}} =\mathrm{47} \\ $$$${x}−{y}=\sqrt{\mathrm{47}} \\ $$$${x}=\frac{\mathrm{7}+\sqrt{\mathrm{47}}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{7}−\sqrt{\mathrm{47}}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{7}+\sqrt{\mathrm{2}}}\:\:=\sqrt{\frac{\mathrm{7}+\sqrt{\mathrm{47}}}{\mathrm{2}}}\:+\sqrt{\frac{\mathrm{7}−\sqrt{\mathrm{47}}}{\mathrm{2}}} \\ $$$${You}\:{can}\:{do}\:{this}\:{same}\:{for}\:{others} \\ $$
Commented by frc2crc last updated on 11/Sep/20
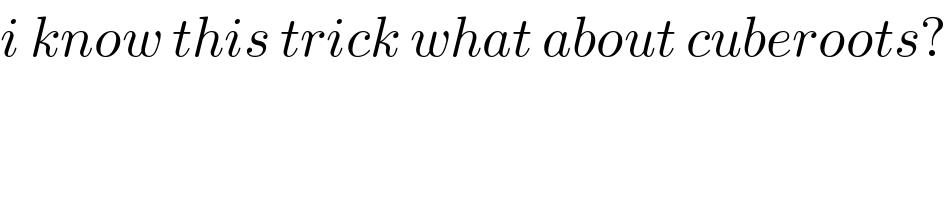
$${i}\:{know}\:{this}\:{trick}\:{what}\:{about}\:{cuberoots}? \\ $$
Commented by Dwaipayan Shikari last updated on 11/Sep/20

$$\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{3}}]{{y}}\:=\sqrt[{\mathrm{3}}]{{a}+\sqrt[{\mathrm{3}}]{{b}}} \\ $$$${x}+{y}+\mathrm{3}\sqrt[{\mathrm{3}}]{{xy}}\:\left(\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{3}}]{{y}}\right)={a}+\sqrt[{\mathrm{3}}]{{b}} \\ $$$${x}+{y}={a} \\ $$$$\mathrm{27}{xy}\left(\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{3}}]{{y}}\right)^{\mathrm{3}} ={b} \\ $$$$\mathrm{27}{xy}\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)={b} \\ $$$${xy}=\frac{{b}}{\mathrm{27}\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)}\:\:\:\:\:\:\:\:\:\left(\:{x}−{y}\right)^{\mathrm{2}} ={a}−\frac{\mathrm{4}{b}}{\mathrm{27}\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)} \\ $$$${x}−{y}=\pm\sqrt{{a}−\frac{\mathrm{4}{b}}{\mathrm{27}\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)}} \\ $$$${x}=\frac{{a}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}−\frac{\mathrm{4}{b}}{\mathrm{27}\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)}} \\ $$$${y}=−\frac{{a}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}−\frac{\mathrm{4}{b}}{\mathrm{27}\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)}} \\ $$$$\sqrt{{a}+\sqrt[{\mathrm{3}}]{{b}}} \\ $$$$=\sqrt[{\mathrm{3}}]{\frac{{a}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}−\frac{\mathrm{4}{b}}{\mathrm{27}\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)}}}\:+\sqrt[{\mathrm{3}}]{−\frac{{a}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}−\frac{\mathrm{4}{b}}{\mathrm{27}\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)}}} \\ $$
