Question Number 4733 by Yozzii last updated on 02/Mar/16

Commented by Yozzii last updated on 02/Mar/16
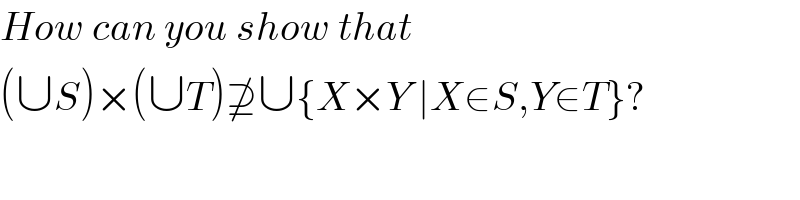
$${How}\:{can}\:{you}\:{show}\:{that}\: \\ $$$$\left(\cup{S}\right)×\left(\cup{T}\right)\nsupseteq\cup\left\{{X}×{Y}\:\mid{X}\in{S},{Y}\in{T}\right\}? \\ $$
Commented by prakash jain last updated on 02/Mar/16

$$\mathrm{From}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{description}\:\mathrm{second}\:\mathrm{part} \\ $$$$\mathrm{along}\:\mathrm{with}\:\mathrm{first}\:\mathrm{part}\:\mathrm{it}\:\mathrm{looks}\:\mathrm{like}\:\mathrm{common} \\ $$$$\mathrm{elements}\:\mathrm{in}\:\mathrm{elements}\:\mathrm{of}\:{S}\:\mathrm{and}\:{T}\:\mathrm{create}\: \\ $$$$\mathrm{extra}\:\mathrm{element}\:\mathrm{in}\:\mathrm{RHS}.\: \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{yet}\:\mathrm{able}\:\mathrm{to}\:\mathrm{identify}\:\mathrm{an}\:\mathrm{element}\:\mathrm{in} \\ $$$$\mathrm{RHS}\:\mathrm{which}\:\mathrm{is}\:\mathrm{not}\:\mathrm{an}\:\mathrm{element}\:\mathrm{in}\:\mathrm{LHS}. \\ $$
Commented by Yozzii last updated on 02/Mar/16

$${Some}\:{special}\:{counter}−{example} \\ $$$${needs}\:{to}\:{be}\:{found}\:{I}\:{think}. \\ $$
Commented by prakash jain last updated on 02/Mar/16
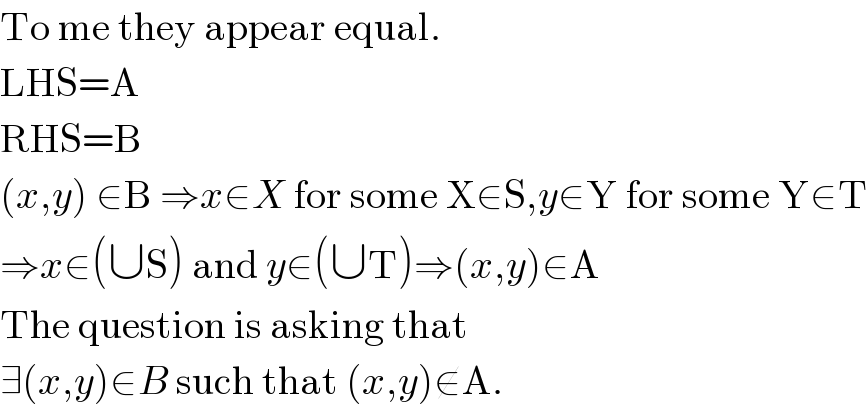
$$\mathrm{To}\:\mathrm{me}\:\mathrm{they}\:\mathrm{appear}\:\mathrm{equal}. \\ $$$$\mathrm{LHS}=\mathrm{A} \\ $$$$\mathrm{RHS}=\mathrm{B} \\ $$$$\left({x},{y}\right)\:\in\mathrm{B}\:\Rightarrow{x}\in{X}\:\mathrm{for}\:\mathrm{some}\:\mathrm{X}\in\mathrm{S},{y}\in\mathrm{Y}\:\mathrm{for}\:\mathrm{some}\:\mathrm{Y}\in\mathrm{T} \\ $$$$\Rightarrow{x}\in\left(\cup\mathrm{S}\right)\:\mathrm{and}\:{y}\in\left(\cup\mathrm{T}\right)\Rightarrow\left({x},{y}\right)\in\mathrm{A} \\ $$$$\mathrm{The}\:\mathrm{question}\:\mathrm{is}\:\mathrm{asking}\:\mathrm{that} \\ $$$$\exists\left({x},{y}\right)\in{B}\:\mathrm{such}\:\mathrm{that}\:\left({x},{y}\right)\notin\mathrm{A}. \\ $$
Commented by Yozzii last updated on 02/Mar/16
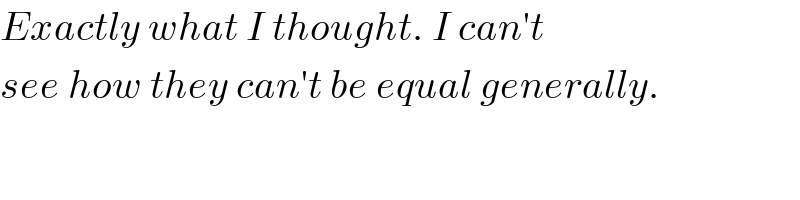
$${Exactly}\:{what}\:{I}\:{thought}.\:{I}\:{can}'{t} \\ $$$${see}\:{how}\:{they}\:{can}'{t}\:{be}\:{equal}\:{generally}. \\ $$
Commented by prakash jain last updated on 04/Mar/16

$$\mathrm{Did}\:\mathrm{you}\:\mathrm{find}\:\mathrm{a}\:\mathrm{counter}\:\mathrm{example}? \\ $$$$\mathrm{123456},\:\mathrm{what}\:\mathrm{is}\:\mathrm{your}\:\mathrm{opinion}? \\ $$
Commented by 123456 last updated on 04/Mar/16
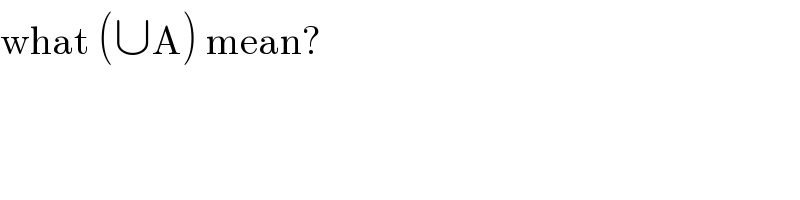
$$\mathrm{what}\:\left(\cup\mathrm{A}\right)\:\mathrm{mean}? \\ $$
Commented by Yozzii last updated on 04/Mar/16
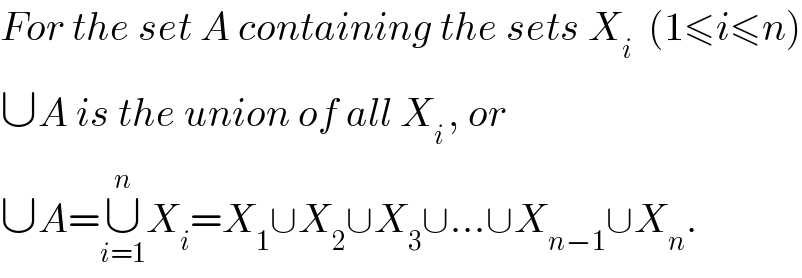
$${For}\:{the}\:{set}\:{A}\:{containing}\:{the}\:{sets}\:{X}_{{i}} \:\:\left(\mathrm{1}\leqslant{i}\leqslant{n}\right) \\ $$$$\cup{A}\:{is}\:{the}\:{union}\:{of}\:{all}\:{X}_{{i}\:} ,\:{or}\: \\ $$$$\cup{A}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\cup}}{X}_{{i}} ={X}_{\mathrm{1}} \cup{X}_{\mathrm{2}} \cup{X}_{\mathrm{3}} \cup…\cup{X}_{{n}−\mathrm{1}} \cup{X}_{{n}} . \\ $$
Commented by 123456 last updated on 04/Mar/16
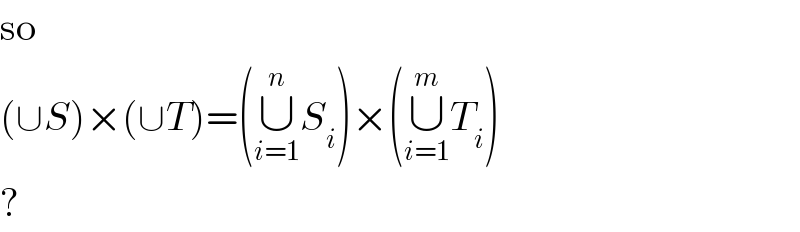
$$\mathrm{so} \\ $$$$\left(\cup{S}\right)×\left(\cup{T}\right)=\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\cup}}{S}_{{i}} \right)×\left(\underset{{i}=\mathrm{1}} {\overset{{m}} {\cup}}{T}_{{i}} \right) \\ $$$$? \\ $$
Commented by Yozzii last updated on 04/Mar/16
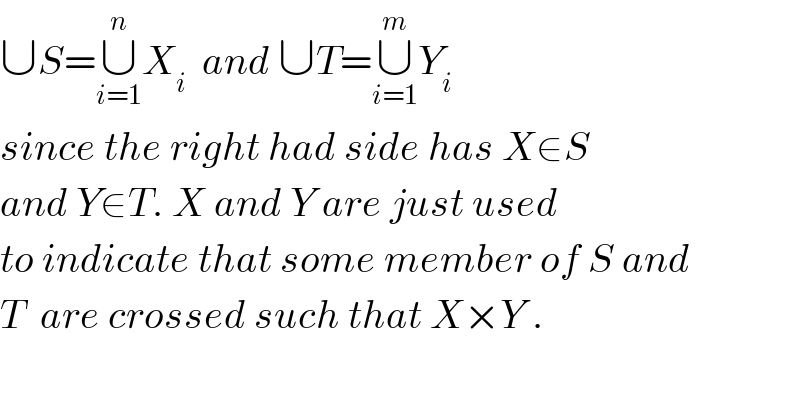
$$\cup{S}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\cup}}{X}_{{i}} \:\:{and}\:\cup{T}=\underset{{i}=\mathrm{1}} {\overset{{m}} {\cup}}{Y}_{{i}} \\ $$$${since}\:{the}\:{right}\:{had}\:{side}\:{has}\:{X}\in{S} \\ $$$${and}\:{Y}\in{T}.\:{X}\:{and}\:{Y}\:{are}\:{just}\:{used} \\ $$$${to}\:{indicate}\:{that}\:{some}\:{member}\:{of}\:{S}\:{and} \\ $$$${T}\:\:{are}\:{crossed}\:{such}\:{that}\:{X}×{Y}\:. \\ $$$$ \\ $$
