Question Number 178994 by Spillover last updated on 23/Oct/22

Commented by Spillover last updated on 23/Oct/22

Answered by mr W last updated on 23/Oct/22
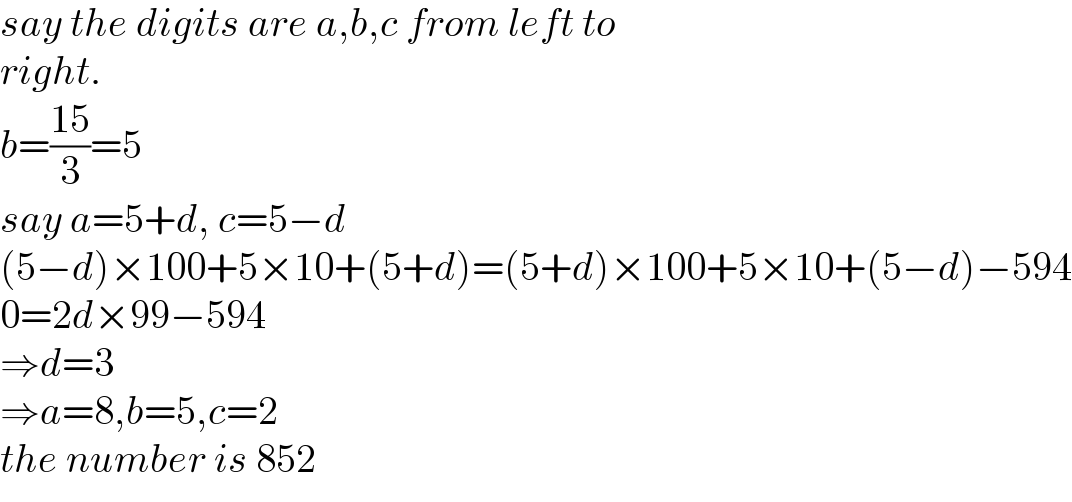
$${say}\:{the}\:{digits}\:{are}\:{a},{b},{c}\:{from}\:{left}\:{to} \\ $$$${right}. \\ $$$${b}=\frac{\mathrm{15}}{\mathrm{3}}=\mathrm{5} \\ $$$${say}\:{a}=\mathrm{5}+{d},\:{c}=\mathrm{5}−{d} \\ $$$$\left(\mathrm{5}−{d}\right)×\mathrm{100}+\mathrm{5}×\mathrm{10}+\left(\mathrm{5}+{d}\right)=\left(\mathrm{5}+{d}\right)×\mathrm{100}+\mathrm{5}×\mathrm{10}+\left(\mathrm{5}−{d}\right)−\mathrm{594} \\ $$$$\mathrm{0}=\mathrm{2}{d}×\mathrm{99}−\mathrm{594} \\ $$$$\Rightarrow{d}=\mathrm{3} \\ $$$$\Rightarrow{a}=\mathrm{8},{b}=\mathrm{5},{c}=\mathrm{2} \\ $$$${the}\:{number}\:{is}\:\mathrm{852} \\ $$
Commented by Spillover last updated on 23/Oct/22

$$\mathrm{thank}\:\mathrm{a}\:\mathrm{lot} \\ $$
Commented by Tawa11 last updated on 23/Oct/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by Rasheed.Sindhi last updated on 23/Oct/22
![Let abc^(−) is requared number. (i) b=((a+c)/2) [∵ a,b,c are in AP] (ii) a+b+c=a+((a+c)/2)+c=15 3a+3c=30⇒a+c=10 (ii) abc^(−) −cba^(−) =594 ⇒100a+c−(100c+a)=594 100a−a+c−100c= ⇒99a−99c=594⇒a−c=6 a=8,c=2,b=((8+2)/2)=5 Required Number=852](https://www.tinkutara.com/question/Q179014.png)
$${Let}\:\overline {{abc}}\:{is}\:{requared}\:{number}. \\ $$$$\left({i}\right)\:{b}=\frac{{a}+{c}}{\mathrm{2}}\: \\ $$$$\left[\because\:{a},{b},{c}\:{are}\:{in}\:{AP}\right] \\ $$$$\left({ii}\right)\:{a}+{b}+{c}={a}+\frac{{a}+{c}}{\mathrm{2}}+{c}=\mathrm{15} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}{a}+\mathrm{3}{c}=\mathrm{30}\Rightarrow{a}+{c}=\mathrm{10} \\ $$$$\left({ii}\right)\:\:\overline {{abc}}−\overline {{cba}}=\mathrm{594} \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{100}{a}+{c}−\left(\mathrm{100}{c}+{a}\right)=\mathrm{594} \\ $$$$\:\:\:\:\:\:\:\mathrm{100}{a}−{a}+{c}−\mathrm{100}{c}= \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{99}{a}−\mathrm{99}{c}=\mathrm{594}\Rightarrow{a}−{c}=\mathrm{6} \\ $$$${a}=\mathrm{8},{c}=\mathrm{2},{b}=\frac{\mathrm{8}+\mathrm{2}}{\mathrm{2}}=\mathrm{5} \\ $$$${Required}\:{Number}=\mathrm{852} \\ $$
Commented by Spillover last updated on 23/Oct/22

$$\mathrm{thank}\:\mathrm{a}\:\mathrm{lot} \\ $$
Commented by SLVR last updated on 23/Oct/22

$${nice}\:{solution}\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 23/Oct/22

$$\mathcal{T}{han}\mathcal{X}\:{sir}! \\ $$
Answered by Spillover last updated on 23/Oct/22

$${a}+{d}\:\:\:{a}\:\:\:{a}−{d} \\ $$$$\mathrm{let}\:\mathrm{hundreds}\:\mathrm{digit}\:\mathrm{a}+\mathrm{d} \\ $$$$\mathrm{tens}\:\mathrm{digit}\:\mathrm{a} \\ $$$$\mathrm{unit}\:\mathrm{digit}\:\mathrm{a}−\mathrm{d} \\ $$$$\mathrm{sum}=\:{a}+{d}\:\:+\:{a}+\:\:\:{a}−{d} \\ $$$$\mathrm{15}=\mathrm{3a}\:\:\:\:\:\mathrm{a}=\mathrm{5} \\ $$$$\mathrm{unreversed}\:\mathrm{digit}\:=\mathrm{100}\left(\mathrm{a}+\mathrm{d}\right)+\mathrm{10a}+\mathrm{1}\left(\mathrm{a}−\mathrm{d}\right)= \\ $$$$\:\:\:\:\:\:\:=\mathrm{555}+\mathrm{99d} \\ $$$$\mathrm{reversed}\:\mathrm{digit}=\mathrm{100}\left(\mathrm{a}−\mathrm{d}\right)+\mathrm{10a}+\mathrm{1}\left(\mathrm{a}+\mathrm{d}\right) \\ $$$$=\mathrm{555}−\mathrm{99d} \\ $$$$\mathrm{594}=\mathrm{unreversed}\:\mathrm{digit}−\mathrm{reversed}\:\mathrm{digit} \\ $$$$\mathrm{594}=\mathrm{555}+\mathrm{99d}−\left[\mathrm{555}−\mathrm{99d}\right. \\ $$$$\mathrm{594}=\mathrm{99d}+\mathrm{99d} \\ $$$$\mathrm{d}=\mathrm{3} \\ $$$${a}+{d}\:\:\:{a}\:\:\:{a}−{d} \\ $$$$\mathrm{5}+\mathrm{3}\:\:\:\mathrm{10}×\mathrm{5}\:\:\:\mathrm{5}−\mathrm{3} \\ $$$$\mathrm{8}\:\:\:\:\:\:\mathrm{50}\:\:\:\:\:\:\mathrm{2} \\ $$$$\mathrm{required}\:\mathrm{number}\:\:\:\mathrm{852} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Oct/22

$$\overline {{abc}}−\overline {{cba}}=+\mathrm{594}\Rightarrow{a}>{c}\:\left({filter}-\mathrm{1}\right) \\ $$$${a},{b},{c}\:{are}\:{in}\:\mathrm{AP}\Rightarrow{b}=\frac{{a}+{c}}{\mathrm{2}}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{9}\right\} \\ $$$$\Rightarrow{a},{c}\in\mathbb{O}\:\vee\:{a},{c}\in\mathbb{E}\:\left({filter}-\mathrm{2}\right) \\ $$$$\left({a},{b},{c}\right)=\left({a},\frac{{a}+{c}}{\mathrm{2}},{c}\right)= \\ $$$${filter}-\mathrm{1}\:\&\:{filter}-\mathrm{2}: \\ $$$$\:\left(\mathrm{8},\mathrm{7},\mathrm{6}\right),\left(\mathrm{8},\mathrm{6},\mathrm{4}\right),\left(\mathrm{8},\mathrm{5},\mathrm{2}\right),\left(\mathrm{8},\mathrm{4},\mathrm{0}\right),\left(\mathrm{6},\mathrm{5},\mathrm{4}\right),\left(\mathrm{6},\mathrm{4},\mathrm{2}\right), \\ $$$$\left(\mathrm{6},\mathrm{3},\mathrm{0}\right),\left(\mathrm{4},\mathrm{3},\mathrm{2}\right),\left(\mathrm{4},\mathrm{2},\mathrm{0}\right),\left(\mathrm{2},\mathrm{1},\mathrm{0}\right) \\ $$$$\left(\mathrm{9},\mathrm{8},\mathrm{7}\right),\left(\mathrm{9},\mathrm{7},\mathrm{5}\right),\left(\mathrm{9},\mathrm{6},\mathrm{3}\right),\left(\mathrm{9},\mathrm{5},\mathrm{1}\right),\left(\mathrm{7},\mathrm{6},\mathrm{5}\right),\left(\mathrm{7},\mathrm{5},\mathrm{3}\right),\left(\mathrm{7},\mathrm{4},\mathrm{1}\right), \\ $$$$\left(\mathrm{5},\mathrm{4},\mathrm{3}\right),\left(\mathrm{5},\mathrm{3},\mathrm{1}\right),\left(\mathrm{3},\mathrm{2},\mathrm{1}\right) \\ $$$${filter}-\mathrm{3}:\:{a}+{b}+{c}=\mathrm{15}: \\ $$$$\left(\mathrm{8},\mathrm{5},\mathrm{2}\right),\left(\mathrm{6},\mathrm{5},\mathrm{4}\right),\left(\mathrm{9},\mathrm{5},\mathrm{1}\right),\left(\mathrm{7},\mathrm{5},\mathrm{3}\right) \\ $$$${filter}-\mathrm{4}:\:\overline {{abc}}−\overline {{cba}}=\mathrm{594}\:: \\ $$$$\mathrm{852}−\mathrm{258}=\mathrm{594}\:\checkmark \\ $$$$\mathrm{654}−\mathrm{456}=\mathrm{198}\:× \\ $$$$\mathrm{951}−\mathrm{159}=\mathrm{792}\:× \\ $$$$\mathrm{753}−\mathrm{357}=\mathrm{396}\:× \\ $$$${Completely}\:{Filtered}: \\ $$$$\:\:\:\:\mathrm{852}\:\:\:\blacktriangleleft\mathrm{Ans} \\ $$$$\mathrm{Changing}\:\mathrm{order}\:\mathrm{of}\:\mathrm{filters}\:\mathrm{may} \\ $$$$\mathrm{make}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{more}\:\mathrm{efficient}. \\ $$
