Question Number 4750 by 123456 last updated on 04/Mar/16
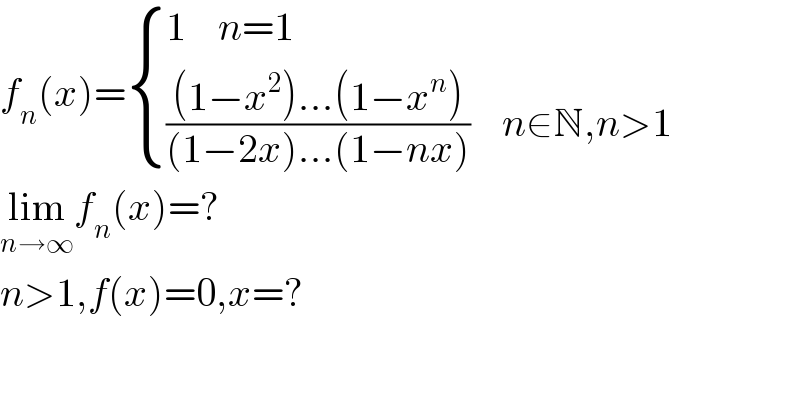
$${f}_{{n}} \left({x}\right)=\begin{cases}{\mathrm{1}\:\:\:\:{n}=\mathrm{1}}\\{\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)…\left(\mathrm{1}−{x}^{{n}} \right)}{\left(\mathrm{1}−\mathrm{2}{x}\right)…\left(\mathrm{1}−{nx}\right)}\:\:\:\:{n}\in\mathbb{N},{n}>\mathrm{1}}\end{cases} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{f}_{{n}} \left({x}\right)=? \\ $$$${n}>\mathrm{1},{f}\left({x}\right)=\mathrm{0},{x}=? \\ $$
Commented by prakash jain last updated on 06/Mar/16
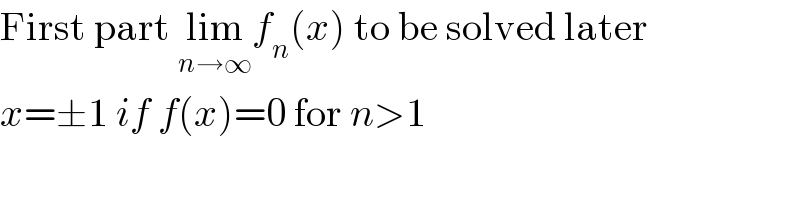
$$\mathrm{First}\:\mathrm{part}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{f}_{{n}} \left({x}\right)\:\mathrm{to}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{later} \\ $$$${x}=\pm\mathrm{1}\:{if}\:{f}\left({x}\right)=\mathrm{0}\:\mathrm{for}\:{n}>\mathrm{1} \\ $$
