Question Number 113714 by mathdave last updated on 14/Sep/20
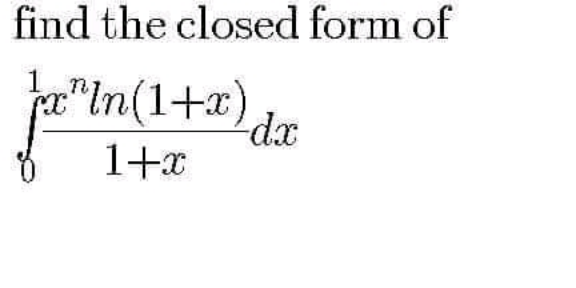
Answered by Olaf last updated on 15/Sep/20
![I_n = ∫_0 ^1 ((x^n ln(1+x))/(1+x))dx I_0 = ∫_0 ^1 ((ln(1+x)dx)/(1+x)) I_0 = [(1/2)ln^2 (1+x)]_0 ^1 = (1/2)ln^2 2 I_(n+1) +I_n = ∫_0 ^1 ((x^(n+1) +x^n )/(1+x))ln(1+x)dx I_(n+1) +I_n = ∫_0 ^1 x^n ln(1+x)dx (1/(1+x)) = Σ_(k=0) ^∞ (−1)^k x^k ln(1+x) = Σ_(k=0) ^∞ (((−1)^k x^(k+1) )/(k+1)), ∣x∣<1 I_(n+1) +I_n = ∫_0 ^1 x^n Σ_(k=0) ^∞ (((−1)^k x^(k+1) )/(k+1))dx I_(n+1) +I_n = ∫_0 ^1 Σ_(k=0) ^∞ (((−1)^k x^(n+k+1) )/(k+1))dx I_(n+1) +I_n = [Σ_(k=0) ^∞ (((−1)^k x^(n+k+1) )/((k+1)(n+k+1)))]_0 ^1 I_(n+1) +I_n = Σ_(k=0) ^∞ (((−1)^k )/((k+1)(n+k+1))) (1/((k+1)(n+k+1))) = (1/n)((1/(k+1))−(1/(n+k+1))) I_(n+1) +I_n = (1/n)Σ_(k=0) ^∞ (−1)^k ((1/(k+1))−(1/(n+k+1))) ...](https://www.tinkutara.com/question/Q113754.png)
$$\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} \mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$\mathrm{I}_{\mathrm{0}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right){dx}}{\mathrm{1}+{x}} \\ $$$$\mathrm{I}_{\mathrm{0}} \:=\:\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \mathrm{2} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} +\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} +{x}^{{n}} }{\mathrm{1}+{x}}\mathrm{ln}\left(\mathrm{1}+{x}\right){dx} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} +\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \mathrm{ln}\left(\mathrm{1}+{x}\right){dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {x}^{{k}} \\ $$$$\mathrm{ln}\left(\mathrm{1}+{x}\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}},\:\mid{x}\mid<\mathrm{1} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} +\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}{dx} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} +\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{{n}+{k}+\mathrm{1}} }{{k}+\mathrm{1}}{dx} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} +\mathrm{I}_{{n}} \:=\:\left[\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{{n}+{k}+\mathrm{1}} }{\left({k}+\mathrm{1}\right)\left({n}+{k}+\mathrm{1}\right)}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} +\mathrm{I}_{{n}} \:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left({k}+\mathrm{1}\right)\left({n}+{k}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\left({n}+{k}+\mathrm{1}\right)}\:=\:\frac{\mathrm{1}}{{n}}\left(\frac{\mathrm{1}}{{k}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+{k}+\mathrm{1}}\right) \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} +\mathrm{I}_{{n}} \:=\:\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \left(\frac{\mathrm{1}}{{k}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+{k}+\mathrm{1}}\right) \\ $$$$… \\ $$
Commented by mathdave last updated on 15/Sep/20
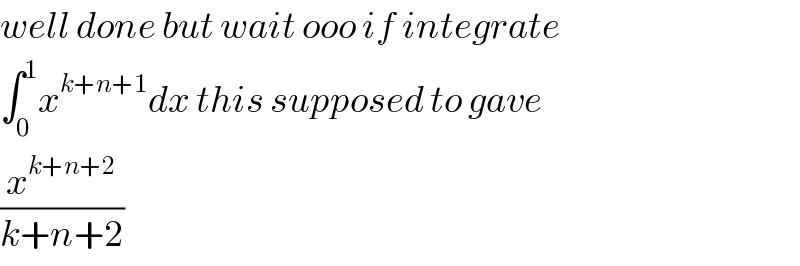
$${well}\:{done}\:{but}\:{wait}\:{ooo}\:{if}\:{integrate}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}+{n}+\mathrm{1}} {dx}\:{this}\:{supposed}\:{to}\:{gave} \\ $$$$\frac{{x}^{{k}+{n}+\mathrm{2}} }{{k}+{n}+\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
