Menu Close

If-1-a-2-1-b-2-1-c-2-1-ab-1-bc-1-ca-then-prove-that-a-b-c-

Tinku Tara 0 Comments
Pin




Question Number 70312 by Shamim last updated on 03/Oct/19
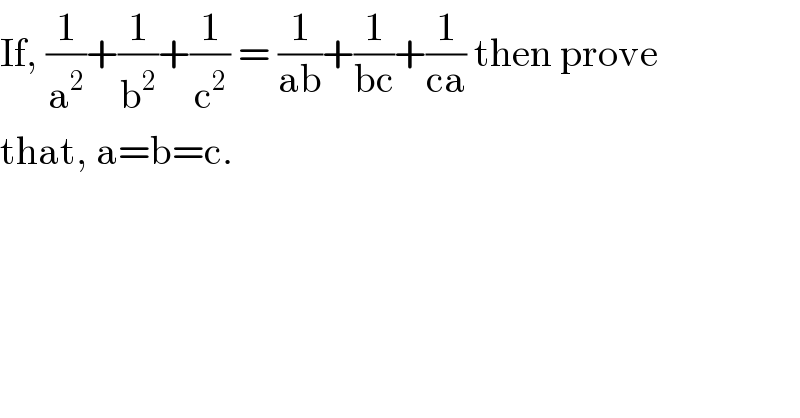
If, (1/a^2 )+(1/b^2 )+(1/c^2 ) = (1/(ab))+(1/(bc))+(1/(ca)) then prove that, a=b=c.
$$\mathrm{If},\:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{c}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{ab}}+\frac{\mathrm{1}}{\mathrm{bc}}+\frac{\mathrm{1}}{\mathrm{ca}}\:\mathrm{then}\:\mathrm{prove}\: \\ $$$$\mathrm{that},\:\mathrm{a}=\mathrm{b}=\mathrm{c}. \\ $$
Commented by MJS last updated on 03/Oct/19
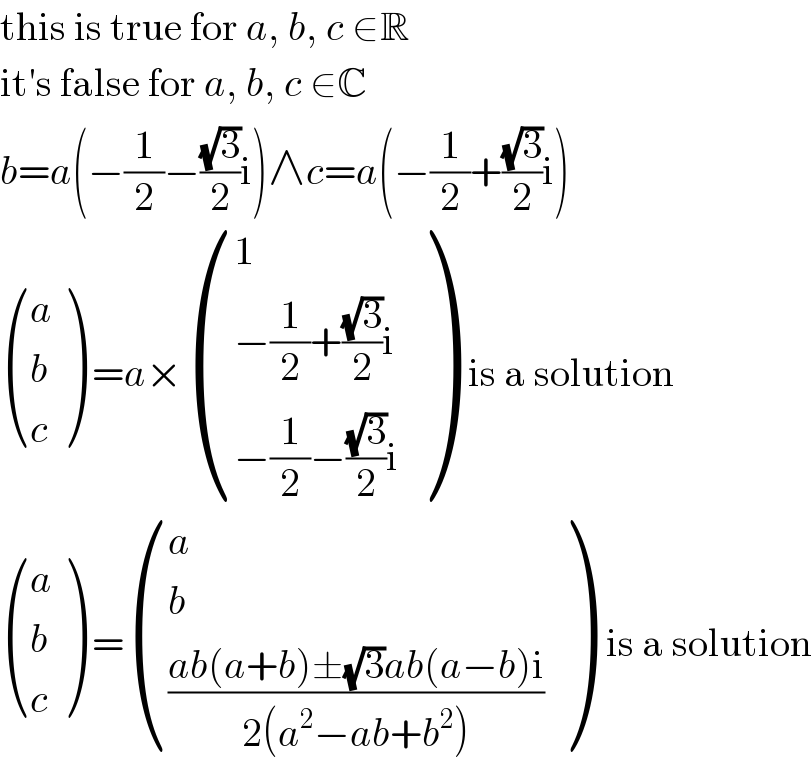
this is true for a, b, c ∈R it′s false for a, b, c ∈C b=a(−(1/2)−((√3)/2)i)∧c=a(−(1/2)+((√3)/2)i) ((a),(b),(c) ) =a× ((1),((−(1/2)+((√3)/2)i)),((−(1/2)−((√3)/2)i)) ) is a solution ((a),(b),(c) ) = ((a),(b),(((ab(a+b)±(√3)ab(a−b)i)/(2(a^2 −ab+b^2 )))) ) is a solution
$$\mathrm{this}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:{a},\:{b},\:{c}\:\in\mathbb{R} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{false}\:\mathrm{for}\:{a},\:{b},\:{c}\:\in\mathbb{C} \\ $$$${b}={a}\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\wedge{c}={a}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right) \\ $$$$\begin{pmatrix}{{a}}\\{{b}}\\{{c}}\end{pmatrix}\:={a}×\begin{pmatrix}{\mathrm{1}}\\{−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}}\\{−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}}\end{pmatrix}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$$$\begin{pmatrix}{{a}}\\{{b}}\\{{c}}\end{pmatrix}\:=\begin{pmatrix}{{a}}\\{{b}}\\{\frac{{ab}\left({a}+{b}\right)\pm\sqrt{\mathrm{3}}{ab}\left({a}−{b}\right)\mathrm{i}}{\mathrm{2}\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)}}\end{pmatrix}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$
Answered by $@ty@m123 last updated on 03/Oct/19
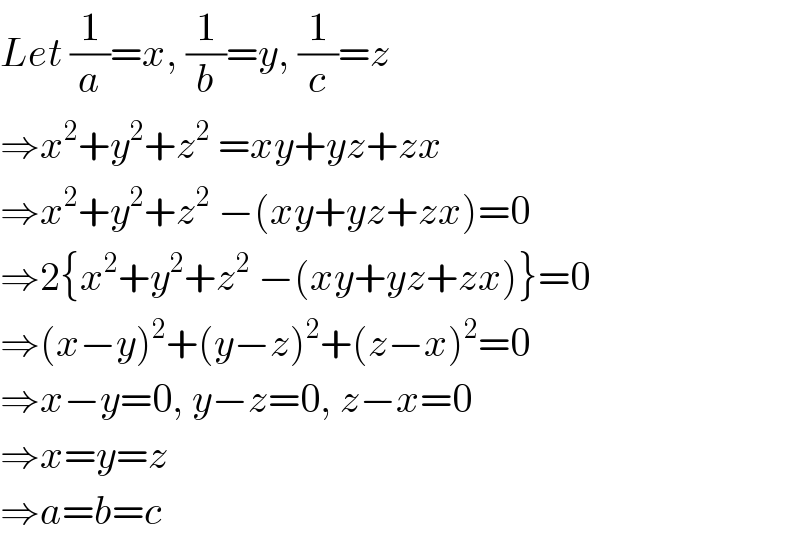
Let (1/a)=x, (1/b)=y, (1/c)=z ⇒x^2 +y^2 +z^2 =xy+yz+zx ⇒x^2 +y^2 +z^2 −(xy+yz+zx)=0 ⇒2{x^2 +y^2 +z^2 −(xy+yz+zx)}=0 ⇒(x−y)^2 +(y−z)^2 +(z−x)^2 =0 ⇒x−y=0, y−z=0, z−x=0 ⇒x=y=z ⇒a=b=c
$${Let}\:\frac{\mathrm{1}}{{a}}={x},\:\frac{\mathrm{1}}{{b}}={y},\:\frac{\mathrm{1}}{{c}}={z} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:={xy}+{yz}+{zx} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:−\left({xy}+{yz}+{zx}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:−\left({xy}+{yz}+{zx}\right)\right\}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{z}\right)^{\mathrm{2}} +\left({z}−{x}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}−{y}=\mathrm{0},\:{y}−{z}=\mathrm{0},\:{z}−{x}=\mathrm{0} \\ $$$$\Rightarrow{x}={y}={z} \\ $$$$\Rightarrow{a}={b}={c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *