Question Number 48506 by Abdo msup. last updated on 24/Nov/18
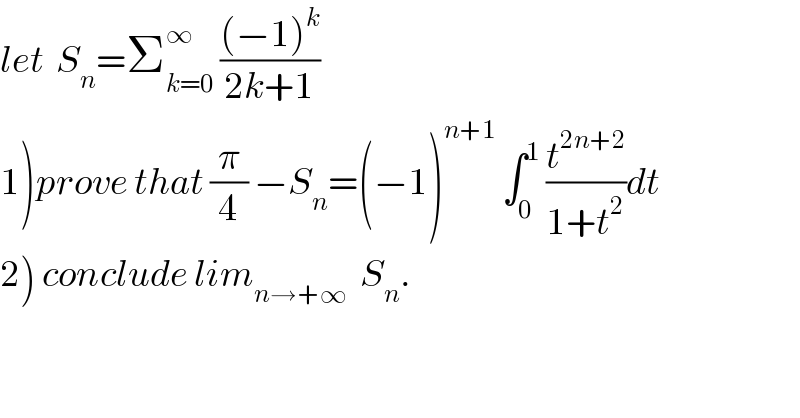
$${let}\:\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}} \\ $$$$\left.\mathrm{1}\right){prove}\:{that}\:\frac{\pi}{\mathrm{4}}\:−{S}_{{n}} =\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{2}\right)\:{conclude}\:{lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} . \\ $$
