Menu Close

Question-131466

Tinku Tara
Pin




Question Number 131466 by Ahmed1hamouda last updated on 05/Feb/21
Commented by Ahmed1hamouda last updated on 05/Feb/21
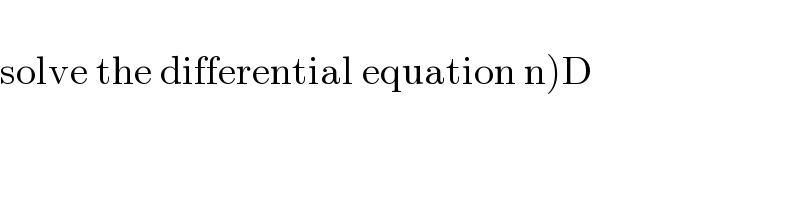
solve the differential equation n)D
$$ \\ $$$$\left.\mathrm{solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation}\:\mathrm{n}\right)\mathrm{D} \\ $$
Answered by EDWIN88 last updated on 05/Feb/21
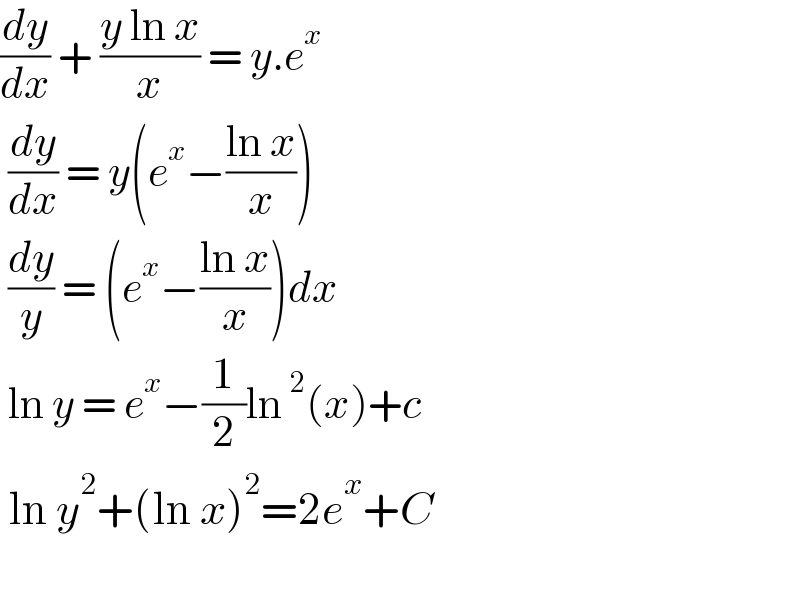
(dy/dx) + ((y ln x)/x) = y.e^x (dy/dx) = y(e^x −((ln x)/x)) (dy/y) = (e^x −((ln x)/x))dx ln y = e^x −(1/2)ln^2 (x)+c ln y^2 +(ln x)^2 =2e^x +C
$$\frac{{dy}}{{dx}}\:+\:\frac{{y}\:\mathrm{ln}\:{x}}{{x}}\:=\:{y}.{e}^{{x}} \\ $$$$\:\frac{{dy}}{{dx}}\:=\:{y}\left({e}^{{x}} −\frac{\mathrm{ln}\:{x}}{{x}}\right) \\ $$$$\:\frac{{dy}}{{y}}\:=\:\left({e}^{{x}} −\frac{\mathrm{ln}\:{x}}{{x}}\right){dx} \\ $$$$\:\mathrm{ln}\:{y}\:=\:{e}^{{x}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:^{\mathrm{2}} \left({x}\right)+{c} \\ $$$$\:\mathrm{ln}\:{y}^{\mathrm{2}} +\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} =\mathrm{2}{e}^{{x}} +{C} \\ $$$$ \\ $$
Commented by Ahmed1hamouda last updated on 05/Feb/21
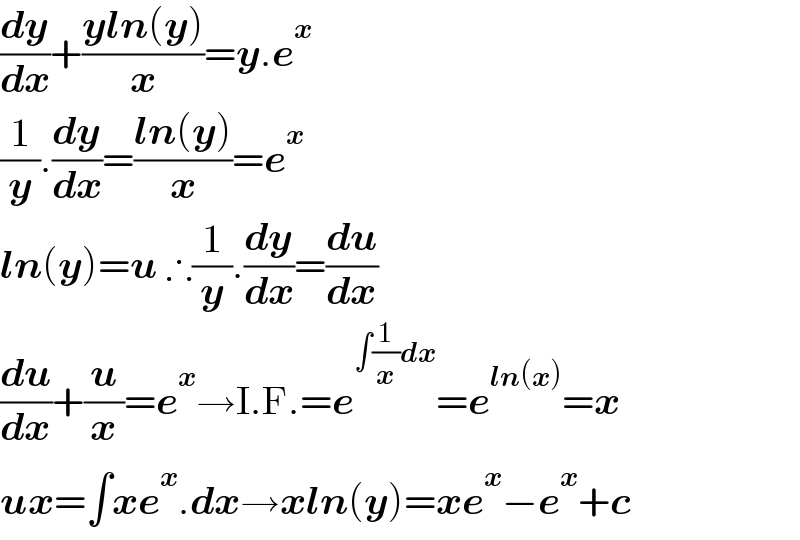
(dy/dx)+((yln(y))/x)=y.e^x (1/y).(dy/dx)=((ln(y))/x)=e^x ln(y)=u ∴(1/y).(dy/dx)=(du/dx) (du/dx)+(u/x)=e^x →I.F.=e^(∫(1/x)dx) =e^(ln(x)) =x ux=∫xe^x .dx→xln(y)=xe^x −e^x +c
$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}+\frac{\boldsymbol{{yln}}\left(\boldsymbol{{y}}\right)}{\boldsymbol{{x}}}=\boldsymbol{{y}}.\boldsymbol{{e}}^{\boldsymbol{{x}}} \\ $$$$\frac{\mathrm{1}}{\boldsymbol{{y}}}.\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\frac{\boldsymbol{{ln}}\left(\boldsymbol{{y}}\right)}{\boldsymbol{{x}}}=\boldsymbol{{e}}^{\boldsymbol{{x}}} \\ $$$$\boldsymbol{{ln}}\left(\boldsymbol{{y}}\right)=\boldsymbol{{u}}\:\therefore\frac{\mathrm{1}}{\boldsymbol{{y}}}.\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\frac{\boldsymbol{{du}}}{\boldsymbol{{dx}}} \\ $$$$\frac{\boldsymbol{{du}}}{\boldsymbol{{dx}}}+\frac{\boldsymbol{{u}}}{\boldsymbol{{x}}}=\boldsymbol{{e}}^{\boldsymbol{{x}}} \rightarrow\mathrm{I}.\mathrm{F}.=\boldsymbol{{e}}^{\int\frac{\mathrm{1}}{\boldsymbol{{x}}}\boldsymbol{{dx}}} =\boldsymbol{{e}}^{\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)} =\boldsymbol{{x}} \\ $$$$\boldsymbol{{ux}}=\int\boldsymbol{{xe}}^{\boldsymbol{{x}}} .\boldsymbol{{dx}}\rightarrow\boldsymbol{{xln}}\left(\boldsymbol{{y}}\right)=\boldsymbol{{xe}}^{\boldsymbol{{x}}} −\boldsymbol{{e}}^{\boldsymbol{{x}}} +\boldsymbol{{c}} \\ $$

Pin