Question Number 114176 by bemath last updated on 17/Sep/20
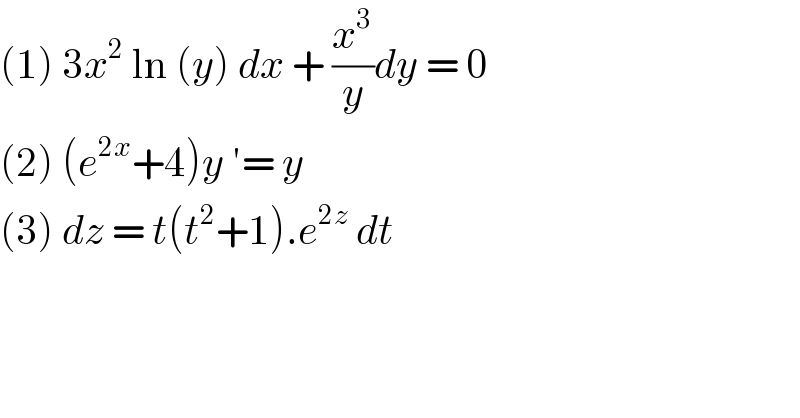
$$\left(\mathrm{1}\right)\:\mathrm{3}{x}^{\mathrm{2}} \:\mathrm{ln}\:\left({y}\right)\:{dx}\:+\:\frac{{x}^{\mathrm{3}} }{{y}}{dy}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\left({e}^{\mathrm{2}{x}} +\mathrm{4}\right){y}\:'=\:{y}\: \\ $$$$\left(\mathrm{3}\right)\:{dz}\:=\:{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right).{e}^{\mathrm{2}{z}} \:{dt}\: \\ $$
Commented by bobhans last updated on 17/Sep/20
![(2) (dy/y) = (dx/(e^(2x) +4)) ⇒∫ (dy/y) = ∫ (dx/(e^(2x) +4)) ⇒ ln (y) = ∫ (dx/(e^(2x) +4)) [ let e^x = 2tan ψ →e^x dx = 2sec^2 ψ dψ ] ⇔ ln (y) = ∫ ((2sec^2 ψ )/(2tan ψ. 4sec^2 ψ))dψ ⇔ ln (y) = (1/4)∫ ((d(sin ψ))/(sin ψ)) ln (y) = (1/4)ln (sin ψ)+c ln (y) = ln (C ((sin ψ))^(1/(4 )) ) ⇒ y = C ((e^x /(4+e^(2x) )))^(1/(4 )) .](https://www.tinkutara.com/question/Q114179.png)
$$\left(\mathrm{2}\right)\:\frac{{dy}}{{y}}\:=\:\frac{{dx}}{{e}^{\mathrm{2}{x}} +\mathrm{4}}\:\Rightarrow\int\:\frac{{dy}}{{y}}\:=\:\int\:\frac{{dx}}{{e}^{\mathrm{2}{x}} +\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{ln}\:\left({y}\right)\:=\:\int\:\frac{{dx}}{{e}^{\mathrm{2}{x}} +\mathrm{4}} \\ $$$$\left[\:{let}\:{e}^{{x}} \:=\:\mathrm{2tan}\:\psi\:\rightarrow{e}^{{x}} \:{dx}\:=\:\mathrm{2sec}\:^{\mathrm{2}} \psi\:{d}\psi\:\right] \\ $$$$\Leftrightarrow\:\mathrm{ln}\:\left({y}\right)\:=\:\int\:\frac{\mathrm{2sec}\:^{\mathrm{2}} \psi\:}{\mathrm{2tan}\:\psi.\:\mathrm{4sec}\:^{\mathrm{2}} \psi}{d}\psi\: \\ $$$$\Leftrightarrow\:\mathrm{ln}\:\left({y}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{{d}\left(\mathrm{sin}\:\psi\right)}{\mathrm{sin}\:\psi} \\ $$$$\:\mathrm{ln}\:\left({y}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{sin}\:\psi\right)+{c}\: \\ $$$$\:\mathrm{ln}\:\left({y}\right)\:=\:\mathrm{ln}\:\left({C}\:\sqrt[{\mathrm{4}\:}]{\mathrm{sin}\:\psi}\:\right)\:\Rightarrow\:{y}\:=\:{C}\:\sqrt[{\mathrm{4}\:}]{\frac{{e}^{{x}} }{\mathrm{4}+{e}^{\mathrm{2}{x}} }}.\: \\ $$
Answered by bobhans last updated on 17/Sep/20
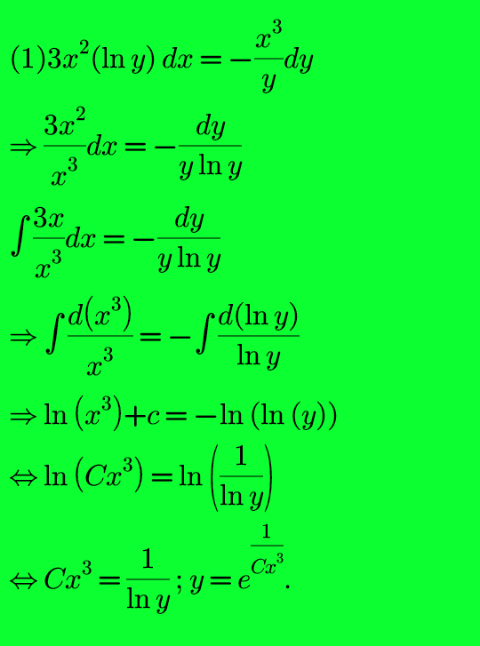
Answered by Dwaipayan Shikari last updated on 17/Sep/20
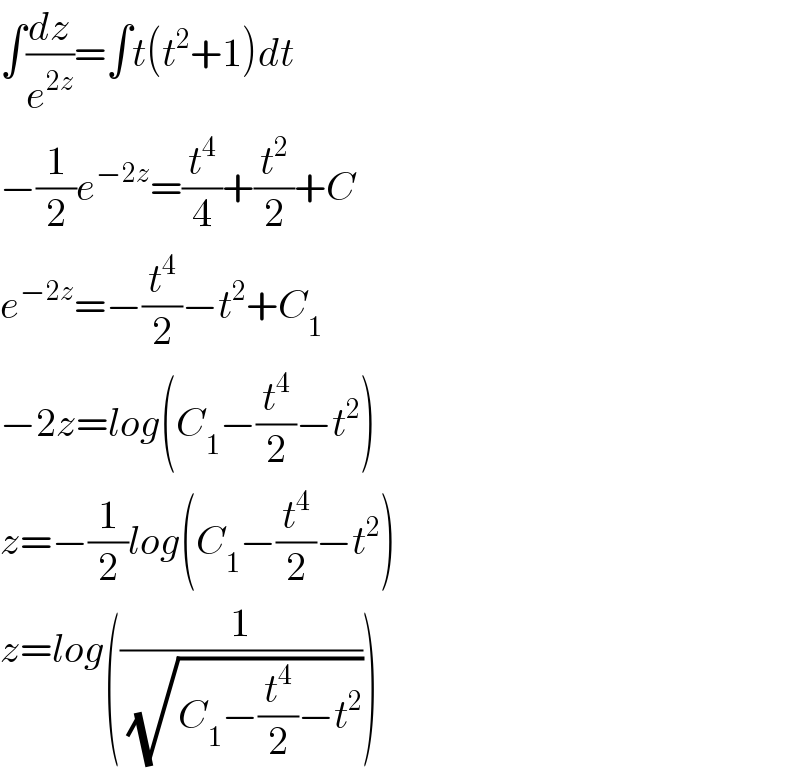
$$\int\frac{{dz}}{{e}^{\mathrm{2}{z}} }=\int{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right){dt} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}{z}} =\frac{{t}^{\mathrm{4}} }{\mathrm{4}}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+{C} \\ $$$${e}^{−\mathrm{2}{z}} =−\frac{{t}^{\mathrm{4}} }{\mathrm{2}}−{t}^{\mathrm{2}} +{C}_{\mathrm{1}} \\ $$$$−\mathrm{2}{z}={log}\left({C}_{\mathrm{1}} −\frac{{t}^{\mathrm{4}} }{\mathrm{2}}−{t}^{\mathrm{2}} \right) \\ $$$${z}=−\frac{\mathrm{1}}{\mathrm{2}}{log}\left({C}_{\mathrm{1}} −\frac{{t}^{\mathrm{4}} }{\mathrm{2}}−{t}^{\mathrm{2}} \right) \\ $$$${z}={log}\left(\frac{\mathrm{1}}{\:\sqrt{{C}_{\mathrm{1}} −\frac{{t}^{\mathrm{4}} }{\mathrm{2}}−{t}^{\mathrm{2}} }}\right) \\ $$
Answered by mathmax by abdo last updated on 18/Sep/20
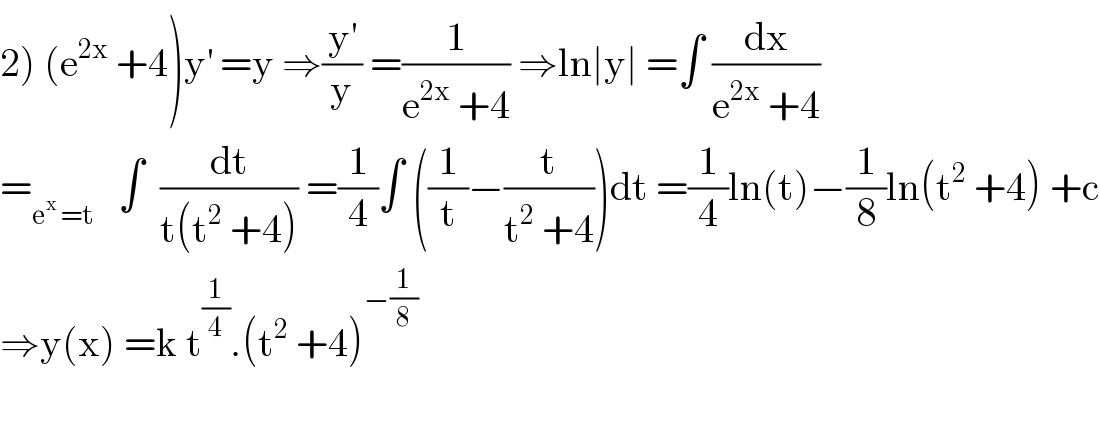
$$\left.\mathrm{2}\right)\:\left(\mathrm{e}^{\mathrm{2x}} \:+\mathrm{4}\right)\mathrm{y}^{'} \:=\mathrm{y}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2x}} \:+\mathrm{4}}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=\int\:\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{2x}} \:+\mathrm{4}} \\ $$$$=_{\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}} \:\:\:\int\:\:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}}\int\:\left(\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}}\right)\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{t}\right)−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}\right)\:+\mathrm{c} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{k}\:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}} .\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}\right)^{−\frac{\mathrm{1}}{\mathrm{8}}} \\ $$$$ \\ $$
