Question Number 114235 by Aina Samuel Temidayo last updated on 18/Sep/20
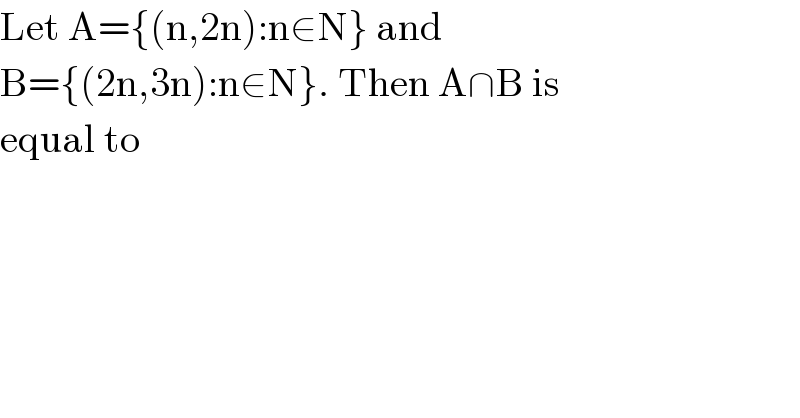
$$\mathrm{Let}\:\mathrm{A}=\left\{\left(\mathrm{n},\mathrm{2n}\right):\mathrm{n}\in\mathrm{N}\right\}\:\mathrm{and} \\ $$$$\mathrm{B}=\left\{\left(\mathrm{2n},\mathrm{3n}\right):\mathrm{n}\in\mathrm{N}\right\}.\:\mathrm{Then}\:\mathrm{A}\cap\mathrm{B}\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to} \\ $$
Answered by 1549442205PVT last updated on 18/Sep/20

$$\mathrm{A}\cap\mathrm{B}=\left(\mathrm{0},\mathrm{0}\right)\mathrm{since} \\ $$$$\left(\mathrm{0},\mathrm{0}\right)=\left(\mathrm{0};\mathrm{2}.\mathrm{0}\right)=\left(\mathrm{2}.\mathrm{0};\mathrm{3}.\mathrm{0}\right) \\ $$
Commented by Aina Samuel Temidayo last updated on 18/Sep/20

$$\mathrm{Not}\:\mathrm{correct}. \\ $$
Commented by MJS_new last updated on 18/Sep/20
$$\mathrm{then}\:\mathrm{what}'\mathrm{s}\:\mathrm{correct}? \\ $$
Commented by 1549442205PVT last updated on 18/Sep/20
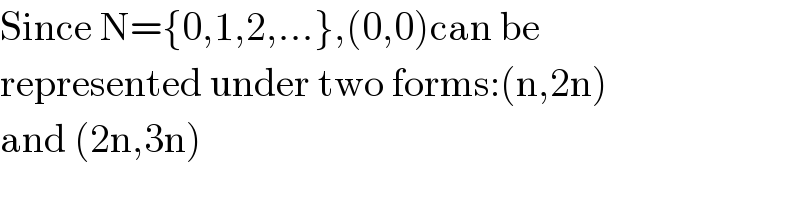
$$\mathrm{Since}\:\mathrm{N}=\left\{\mathrm{0},\mathrm{1},\mathrm{2},…\right\},\left(\mathrm{0},\mathrm{0}\right)\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{represented}\:\mathrm{under}\:\mathrm{two}\:\mathrm{forms}:\left(\mathrm{n},\mathrm{2n}\right) \\ $$$$\mathrm{and}\:\left(\mathrm{2n},\mathrm{3n}\right) \\ $$
Answered by malwaan last updated on 18/Sep/20
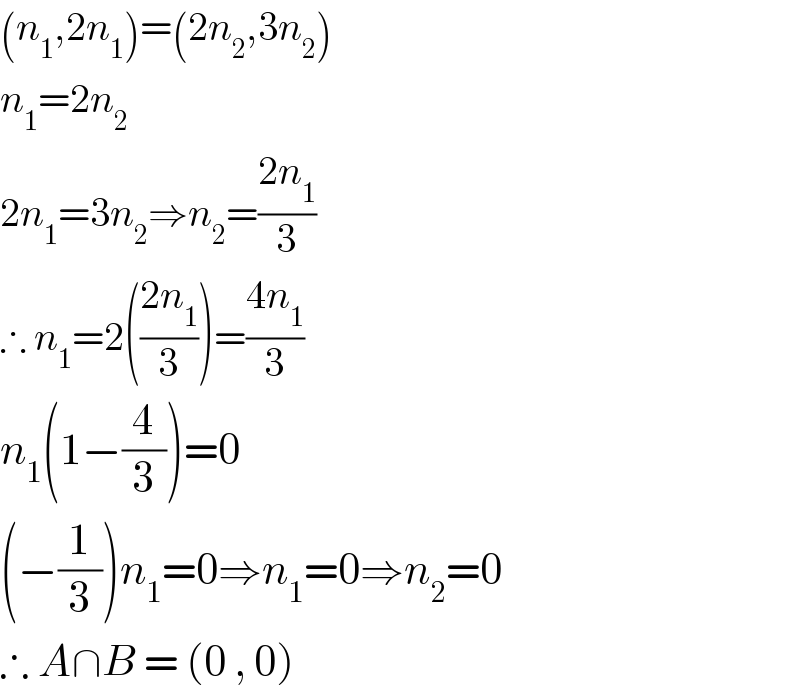
$$\left({n}_{\mathrm{1}} ,\mathrm{2}{n}_{\mathrm{1}} \right)=\left(\mathrm{2}{n}_{\mathrm{2}} ,\mathrm{3}{n}_{\mathrm{2}} \right) \\ $$$${n}_{\mathrm{1}} =\mathrm{2}{n}_{\mathrm{2}} \\ $$$$\mathrm{2}{n}_{\mathrm{1}} =\mathrm{3}{n}_{\mathrm{2}} \Rightarrow{n}_{\mathrm{2}} =\frac{\mathrm{2}{n}_{\mathrm{1}} }{\mathrm{3}} \\ $$$$\therefore\:{n}_{\mathrm{1}} =\mathrm{2}\left(\frac{\mathrm{2}{n}_{\mathrm{1}} }{\mathrm{3}}\right)=\frac{\mathrm{4}{n}_{\mathrm{1}} }{\mathrm{3}} \\ $$$${n}_{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{3}}\right){n}_{\mathrm{1}} =\mathrm{0}\Rightarrow{n}_{\mathrm{1}} =\mathrm{0}\Rightarrow{n}_{\mathrm{2}} =\mathrm{0} \\ $$$$\therefore\:{A}\cap{B}\:=\:\left(\mathrm{0}\:,\:\mathrm{0}\right) \\ $$
Commented by Aina Samuel Temidayo last updated on 19/Sep/20
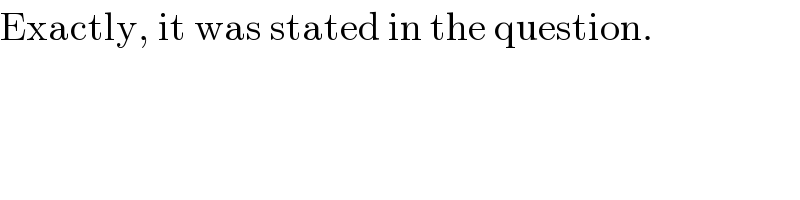
$$\mathrm{Exactly},\:\mathrm{it}\:\mathrm{was}\:\mathrm{stated}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}. \\ $$
Commented by 1549442205PVT last updated on 18/Sep/20
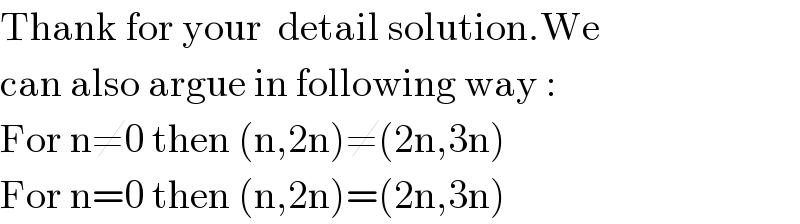
$$\mathrm{Thank}\:\mathrm{for}\:\mathrm{your}\:\:\mathrm{detail}\:\mathrm{solution}.\mathrm{We} \\ $$$$\mathrm{can}\:\mathrm{also}\:\mathrm{argue}\:\mathrm{in}\:\mathrm{following}\:\mathrm{way}\:: \\ $$$$\mathrm{For}\:\mathrm{n}\neq\mathrm{0}\:\mathrm{then}\:\left(\mathrm{n},\mathrm{2n}\right)\neq\left(\mathrm{2n},\mathrm{3n}\right) \\ $$$$\mathrm{For}\:\mathrm{n}=\mathrm{0}\:\mathrm{then}\:\left(\mathrm{n},\mathrm{2n}\right)=\left(\mathrm{2n},\mathrm{3n}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 18/Sep/20
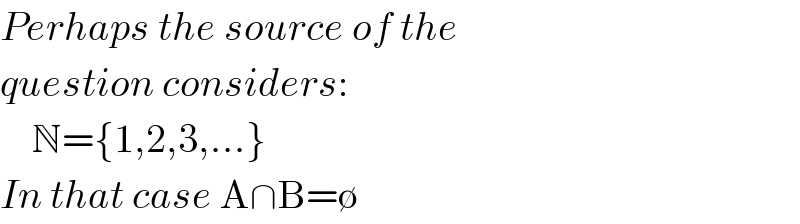
$${Perhaps}\:{the}\:{source}\:{of}\:{the} \\ $$$${question}\:{considers}: \\ $$$$\:\:\:\:\mathbb{N}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},…\right\} \\ $$$${In}\:{that}\:{case}\:\mathrm{A}\cap\mathrm{B}=\emptyset \\ $$
Commented by MJS_new last updated on 19/Sep/20
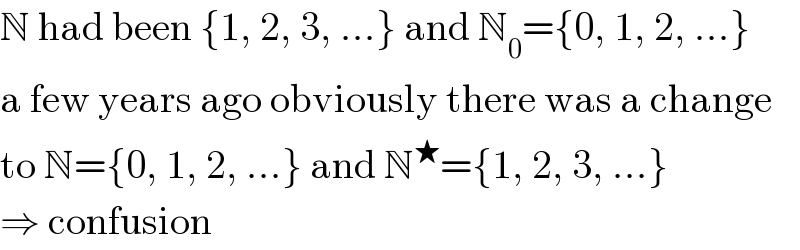
$$\mathbb{N}\:\mathrm{had}\:\mathrm{been}\:\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:…\right\}\:\mathrm{and}\:\mathbb{N}_{\mathrm{0}} =\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:…\right\} \\ $$$$\mathrm{a}\:\mathrm{few}\:\mathrm{years}\:\mathrm{ago}\:\mathrm{obviously}\:\mathrm{there}\:\mathrm{was}\:\mathrm{a}\:\mathrm{change} \\ $$$$\mathrm{to}\:\mathbb{N}=\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:…\right\}\:\mathrm{and}\:\mathbb{N}^{\bigstar} =\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:…\right\} \\ $$$$\Rightarrow\:\mathrm{confusion} \\ $$
