Question Number 114304 by mnjuly1970 last updated on 18/Sep/20
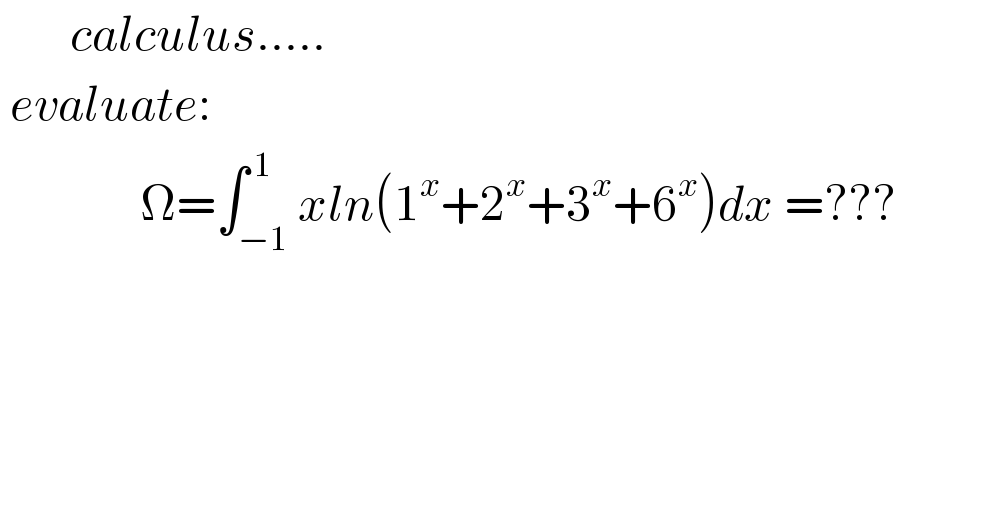
$$\:\:\:\:\:\:\:{calculus}….. \\ $$$$\:{evaluate}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{−\mathrm{1}} ^{\:\mathrm{1}} {xln}\left(\mathrm{1}^{{x}} +\mathrm{2}^{{x}} +\mathrm{3}^{{x}} +\mathrm{6}^{{x}} \right){dx}\:=???\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by MJS_new last updated on 18/Sep/20
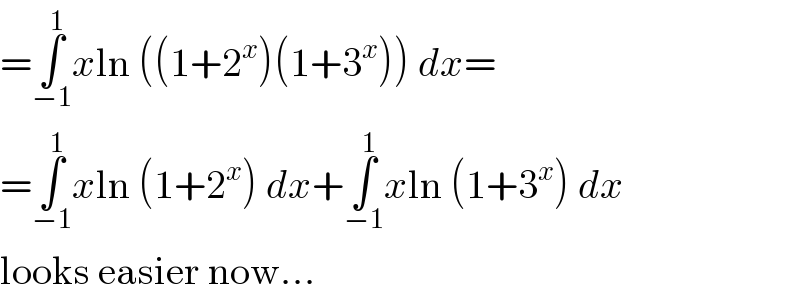
$$=\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}{x}\mathrm{ln}\:\left(\left(\mathrm{1}+\mathrm{2}^{{x}} \right)\left(\mathrm{1}+\mathrm{3}^{{x}} \right)\right)\:{dx}= \\ $$$$=\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}{x}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{2}^{{x}} \right)\:{dx}+\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}{x}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3}^{{x}} \right)\:{dx} \\ $$$$\mathrm{looks}\:\mathrm{easier}\:\mathrm{now}… \\ $$
Commented by Dwaipayan Shikari last updated on 18/Sep/20

$$\frac{{log}\left(\mathrm{6}\right)}{\mathrm{3}} \\ $$
Commented by Dwaipayan Shikari last updated on 18/Sep/20
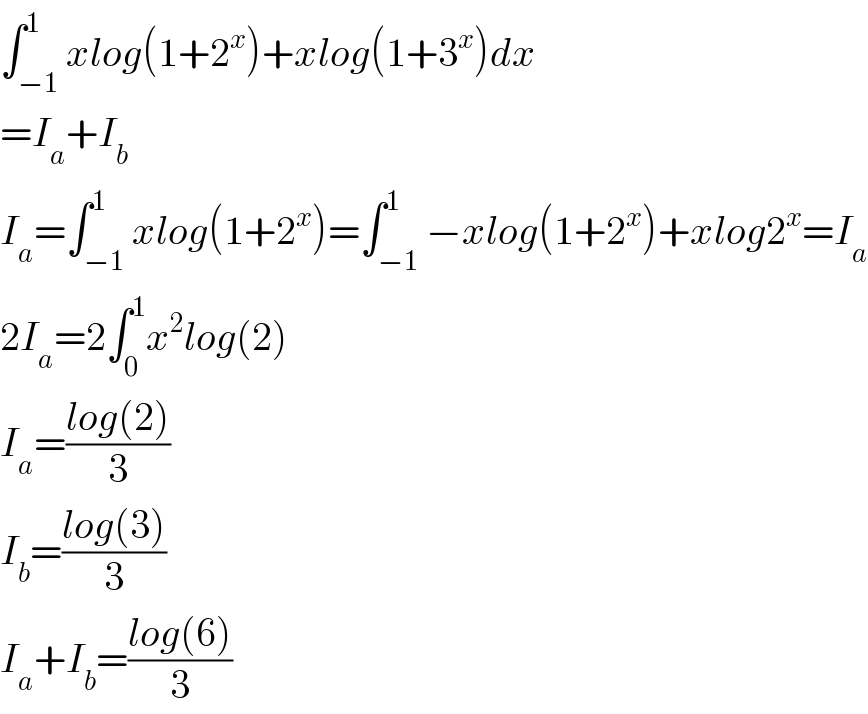
$$\int_{−\mathrm{1}} ^{\mathrm{1}} {xlog}\left(\mathrm{1}+\mathrm{2}^{{x}} \right)+{xlog}\left(\mathrm{1}+\mathrm{3}^{{x}} \right){dx} \\ $$$$={I}_{{a}} +{I}_{{b}} \\ $$$${I}_{{a}} =\int_{−\mathrm{1}} ^{\mathrm{1}} {xlog}\left(\mathrm{1}+\mathrm{2}^{{x}} \right)=\int_{−\mathrm{1}} ^{\mathrm{1}} −{xlog}\left(\mathrm{1}+\mathrm{2}^{{x}} \right)+{xlog}\mathrm{2}^{{x}} ={I}_{{a}} \\ $$$$\mathrm{2}{I}_{{a}} =\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {log}\left(\mathrm{2}\right) \\ $$$${I}_{{a}} =\frac{{log}\left(\mathrm{2}\right)}{\mathrm{3}} \\ $$$${I}_{{b}} =\frac{{log}\left(\mathrm{3}\right)}{\mathrm{3}} \\ $$$${I}_{{a}} +{I}_{{b}} =\frac{{log}\left(\mathrm{6}\right)}{\mathrm{3}} \\ $$
Commented by MJS_new last updated on 18/Sep/20

$$\mathrm{yesss}!\:\mathrm{I}\:\mathrm{had}\:\mathrm{been}\:\mathrm{focused}\:\mathrm{on}\:\mathrm{the}\:\mathrm{integral}, \\ $$$$\mathrm{forgot}\:\mathrm{the}\:\mathrm{symmetric}\:\mathrm{borders}… \\ $$
Commented by mnjuly1970 last updated on 18/Sep/20

$${grateful}\:..= \\ $$
Commented by mnjuly1970 last updated on 18/Sep/20

$${thank}\:{you}\:…. \\ $$
