Question Number 179991 by mnjuly1970 last updated on 05/Nov/22

Answered by mindispower last updated on 05/Nov/22
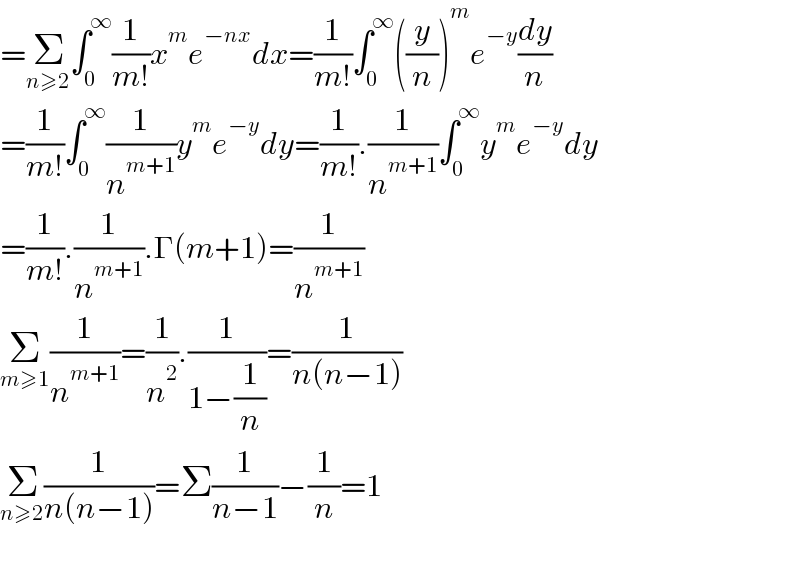
$$=\underset{{n}\geqslant\mathrm{2}} {\sum}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{m}!}{x}^{{m}} {e}^{−{nx}} {dx}=\frac{\mathrm{1}}{{m}!}\int_{\mathrm{0}} ^{\infty} \left(\frac{{y}}{{n}}\right)^{{m}} {e}^{−{y}} \frac{{dy}}{{n}} \\ $$$$=\frac{\mathrm{1}}{{m}!}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}^{{m}+\mathrm{1}} }{y}^{{m}} {e}^{−{y}} {dy}=\frac{\mathrm{1}}{{m}!}.\frac{\mathrm{1}}{{n}^{{m}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} {y}^{{m}} {e}^{−{y}} {dy} \\ $$$$=\frac{\mathrm{1}}{{m}!}.\frac{\mathrm{1}}{{n}^{{m}+\mathrm{1}} }.\Gamma\left({m}+\mathrm{1}\right)=\frac{\mathrm{1}}{{n}^{{m}+\mathrm{1}} } \\ $$$$\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{{m}+\mathrm{1}} }=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }.\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{n}}}=\frac{\mathrm{1}}{{n}\left({n}−\mathrm{1}\right)} \\ $$$$\underset{{n}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{1}}{{n}\left({n}−\mathrm{1}\right)}=\Sigma\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}}=\mathrm{1} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 05/Nov/22

$$\:\:\:\:\:{mercey}\:{sir} \\ $$
