Question Number 114722 by Dwaipayan Shikari last updated on 20/Sep/20
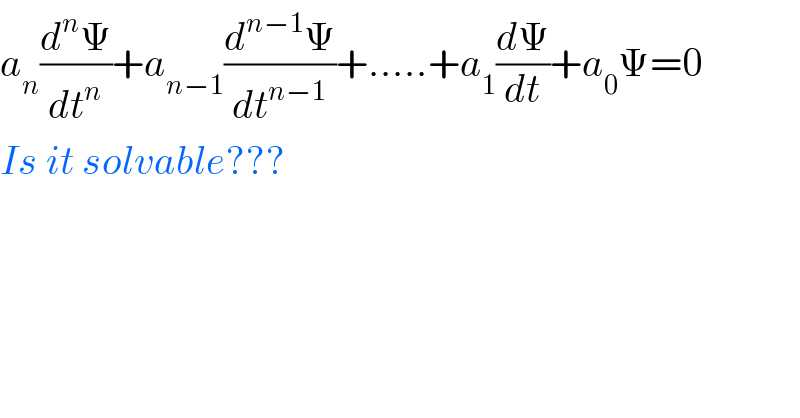
$${a}_{{n}} \frac{{d}^{{n}} \Psi}{{dt}^{{n}} }+{a}_{{n}−\mathrm{1}} \frac{{d}^{{n}−\mathrm{1}} \Psi}{{dt}^{{n}−\mathrm{1}} }+…..+{a}_{\mathrm{1}} \frac{{d}\Psi}{{dt}}+{a}_{\mathrm{0}} \Psi=\mathrm{0} \\ $$$${Is}\:{it}\:{solvable}??? \\ $$
Answered by Olaf last updated on 21/Sep/20

$$\mathrm{Only}\:\mathrm{in}\:\mathrm{special}\:\mathrm{cases}. \\ $$$$\mathrm{Not}\:\mathrm{in}\:\mathrm{the}\:\mathrm{general}\:\mathrm{case} \\ $$$$\mathrm{because}\:\mathrm{you}\:\mathrm{need}\:\mathrm{to}\:\mathrm{know} \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{polynomial} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{k}} {x}^{{k}} \\ $$$$ \\ $$
Answered by aleks041103 last updated on 21/Sep/20

$${Not}\:{in}\:{general}…{at}\:{least}\:{not}\:{analyticaly}: \\ $$$${let}\:\psi={e}^{{rt}} \:{be}\:{a}\:{solution} \\ $$$${then} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} \frac{{d}^{{i}} \psi}{{dt}^{{i}} }=\mathrm{0} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {r}^{{i}} {e}^{{rt}} =\left(\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {r}^{{i}} \right){e}^{{rt}} =\mathrm{0} \\ $$$${since}\:{e}^{{rt}} \neq\mathrm{0},\:{then} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {r}^{{i}} =\mathrm{0} \\ $$$${this}\:{is}\:{a}\:{polynomial}\:{of}\:{degree}\:{n}\:{and} \\ $$$${by}\:{the}\:{fundamental}\:{theory}\:{of}\:{algebra} \\ $$$${it}\:{has}\:{n}\:{complex}\:{solutions}\:{which}\:{we} \\ $$$${will}\:{denote}\:{with}\:{r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} ,\:…\:{r}_{{n}} . \\ $$$${Because}\:{the}\:{ODE}\:{is}\:{linear},\:{then}\:{any} \\ $$$${linear}\:{combination}\:{of}\:{the}\:{n}\:{possible} \\ $$$${solutions}\:{will}\:{be}\:{a}\:{solution}: \\ $$$$\Psi=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{A}_{{k}} {e}^{{r}_{{k}} {t}} \\ $$$${In}\:{general}\:{an}\:{ODE}\:{of}\:{degree}\:{n},\:{that} \\ $$$${is}\:{it}\:{has}\:{an}\:{n}−{th}\:{derivative},\:{will}, \\ $$$${figiratively}\:{said},\:{need}\:{to}\:{be}\:{integrated} \\ $$$${n}\:{times},\:{which}\:{means}\:{that}\:{in}\:{the}\:{end} \\ $$$${we}\:{will}\:{end}\:{up}\:{with}\:{n}\:{constants}\:{of} \\ $$$${integration}\: \\ $$$${Since}\:{our}\:{solution}\:{also}\:{has}\:{n}\:{constants} \\ $$$${then}\:{our}\:{solution}\:{is}\:{the}\:{general}\:{solution}. \\ $$$${To}\:{recap}: \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} \frac{{d}^{{i}} \Psi}{{dt}^{{i}} }=\mathrm{0}\:\Rightarrow\:\Psi=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{A}_{{k}} {e}^{{r}_{{k}} {t}} , \\ $$$${where}\:{for}\:\forall{k}=\mathrm{1},\:…\:{n},\:\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {r}_{{k}} ^{{i}} =\mathrm{0}\: \\ $$$${and}\:{the}\:{constants}\:{A}_{{k}} \:{are}\:{fixed}\:{using} \\ $$$${the}\:{initial}\left({or}\:{possibly}\:{bondary}\right) \\ $$$${conditions}. \\ $$$$ \\ $$
